3.Алгоритм нумерации событий.

Для нумерации событий применяется сл способ. Вычеркиваются все работы, выходящие из события с номером "0", и просматриваются все события, в которых оканчиваются эти вычеркнутые работы. Среди просмотренных находятся события, которые не имеют входящих в них работ (за исключением уже вычеркнутых). Они называются событиями первого ранга и обозначаются (вообще, в произвольном порядке) числами натурального ряда, начиная с единицы (на рис. 14.1 это событие 1). Затем вычеркиваются все работы, выходящие из событий первого ранга, и среди них находятся события, не имеющие входящих работ (кроме вычеркнутых). Это — события второго ранга, которые нумеруются следующими числами натурального ряда (например, 2 и 3 на рис. 14.1). Проделав таким способом шаг, определяют события - го ранга, и просматривая события, в которых эти работы заканчиваются, выбирают события, не имеющие ни одной входящей в них работы (кроме вычеркнутых). Это события -го ранга, и нумеруются они последовательными числами натурального ряда, начиная с наименьшего, еще не использованного числа при предыдущей нумерации на -м шаге.

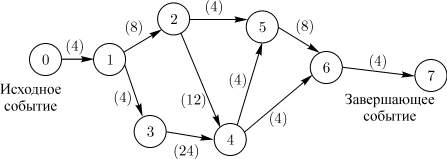
Рис. 14.1. 

Сетевой график содержит конечное число событий. Поскольку в процессе вычеркивания движение осуществляется в направлении стрелок (работ), никакое предшествующее событие не может получить номер, больший, чем любое последующее. Всегда найдется хотя бы одно событие соответствующего ранга, и все события получат номера за конечное число шагов.

Работа обычно кодируется номерами событий, между которыми они заключены, то есть парой , где — номер предшествующего события, — номер последующего события.

В одно и то же событие могут входить (выходить) одна или несколько работ. Поэтому свершение события зависит от завершения самой длительной из всех входящих в него работ. Взаимосвязь между работами определяется тем, что начало последующей работы обусловлено окончанием предыдущей. Отсюда следует, что нет работ, не связанных началом и окончанием с другими работами через события. Последовательные работы и события формируют цепочки (пути), которые ведут от исходного события сетевого графика к завершающему. Например, путь сетевого графика, показанного на (рис.14.1), включает в себя события и работы .

4.Алгоритм расчета плана ранних и поздних сроков свершения событий. Примеры расчета.

Ранний срок (ожидаемый момент) осуществления j-го события представляет собой момент времени, раньше которого событие произойти не может и рассчитывается по формуле

.                                       (3.1)

 Поздний срок (предельный момент) осуществления i-го собы­тия показывает максимальную задержку во времени наступления данного события:

 

.                                      (3.2)

 Одно из важнейших понятий сетевого графика – понятие пути L.

Критический путь – последовательность работ между начальными и конечными событиями сети, имеющих наибольшую продолжительность во времени. Минимальное время, необходимое для выполнения проекта, запланированного сетевым графиком, равно длине критического пути. Сетевой график может содержать не один, а несколько критических путей. Критическими называются также работы и события, расположенные на этом пути. Резервный интервал от t до t* для событий, лежащих на критическом пути, равен 0. Для завершающего события сетевого графика поздний срок свершения события должен равняться его раннему сроку, т. е. t_п = t*_п.

Длина критического пути равна раннему сроку свершения завершающего события, т. е. t_кр = t_п = t*_п.

Первый этап - пронумеровать все события сети так, чтобы для каждой операции использовался алгоритм нумерации событий. Переносятся исходные данные с сетевого графи­ка в таблицу. Работы зано­сятся в порядке возрастания номеров начальных событий.

Второй этап - рассчитываются ранние параметры работ, расчет ведется от исходного события к завер­шающему. Раннее начало всех работ, выходящих из исходного события, принимается равным нулю. В дальнейшем раннее начало принимается равным наибольшему значению из ранних окончаний, входящих в на­чальное событие работ. Так, для работы 4-5 раннее начало равно

Раннее окончание работ равно сумме раннего начала и продолжи­тельности работы.

Третий этап - рассчитываются поздние параметры работ. Расчет ведется, начиная с работ, входящих в за­вершающее событие. Поздний срок окончания этих работ равен мак­симальному сроку из ранних окончаний работ, входящих в завершаю­щее событие. Позднее окончание других работ принимается равным наименьшему значению из поздних начал работ, выходящих из ко­нечного события рассматриваемой работы. Позднее начало работы определяется разностью между ее поздним окончанием и продолжи­тельностью. Хотя бы одна из работ, выходящих из исходного события, имеет позднее начало, равное нулю.