Перечень контрольных вопросов для подготовки к зачету по дисциплине «Модели и методы календарного планирования производства»

Тема №1. Введение в теорию графов. Основные понятия и определения. Компоненты графа. Гамильтоновы и эйлеровы линии. Задача о Кенигсбергских мостах.

1.Определение графа, основные его элементы: ребра, вершины. Ориентированный и неориентированный граф. Граф

Граф (или неориентированный граф) — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами). Мультиграф - граф, у которого хотя бы одна пара вершин соединяется более чем 1 дугой (ребром).

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра.

Два ребра называются смежными, если они имеют общую концевую вершину. Два ребра называются кратными, если множества их концевых вершин совпадают.

Ориентированный граф

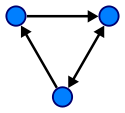
Ориентированный граф G — это упорядоченная пара G: = (V,A), для которой выполнены следующие условия:

• V это множество вершин или узлов,

• A это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v w ведёт от вершины v к вершине w.

Смешанный граф

Смешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G: = (V,E,A), где V, E и A определены так же, как выше.

Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.

2.Графические изображения графа. Пути и цепи.

Путем в графе называется последовательность в которой чередуются вершины и дуги графа. Начинается последовательность с вершины которая называется началом пути и заканчивается вершиной, называемой концом пути. \\\ 2 Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.

Например, для графа изображенного на рисунке, путем будет следующая последовательность: v1 x1 v2 x3 v4 x4 v3, где v1- начало, а v3- конец пути.

 

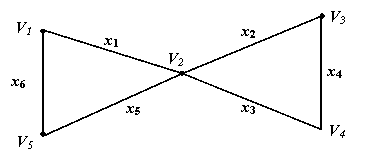
            Замечание. Путь можно записать по последовательности дуг, которые входят в данный путь. Для приведенного выше пути, это будет последовательность: x1 x3 x4. Если дуги имеют кратность 1, то путь можно записать по последовательности вершин, входящих в данный путь. Для приведенного выше пути, это будет последовательность: v1 v2 v4 v3. Длиной пути называется число дуг, входящих в данный путь. Длина приведенного выше пути – 3. Путь называется замкнутым, если начало пути совпадает с концом этого пути.

Определение. Цепью называется путь в котором все дуги различны. Простая цепь – цепь в которой все вершины различны. \\\2 Цепь маршрут, в котором все ребра попарно различны.

3.Гамильтоновы и эйлеровы линии. Гамильтонов путь - содержит все вершины графа. Эйлеров путь - содержащий все ребра графа.

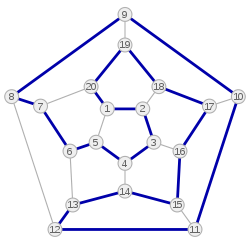
Граф с выделенным циклом Гамильтона

Гамильтоновым путем в графе называется путь, проходящий через каждую вершину графа в точности по одному разу. Теорема. Всякий полный граф является гамильтоновым. Дей­ствительно, он содержит такой простой цикл, которому принадлежат все вершины данного графа. Теорема. Если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие ребра, то он также является гамильтоновым. 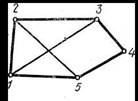                                                                                                                                   На рисунке простой (гамильтонов) цикл выделен жирной линией (1, 2), (2, 3), (3, 4), (4, 5), (5, 1). Заметим также, что если граф имеет один гамильтонов цикл, то он может иметь и другие гамильтоновы циклы. _ Эйлеровым путем в графе называется путь, содержащий все ребра графа. Эйлеровым циклом в графе называется цикл, содержащий все ребра графа.

Связный граф G называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро. Такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Примеры.

Теорема. Если граф G обладает эйлеровым циклом, то он является связным, а все его вершины — чётными. Доказательство Связность графа следует из определения эйлерова цикла. Эйлеров цикл содержит каждое ребро и притом только один раз, поэтому, сколько раз эйлеров путь приведет конец карандаша в вершину, столько и выведет, причем уже по другому ребру. Следовательно, степень каждой вершины графа должна состоять из двух одинаковых слагаемых: одно результат подсчета входов в вершину, другое — выходов.