§6. Задача Коши для уравнения параболического типа.

Формула Пуассона

Задача Коши: Найти решение уравнения

(6:1)

удовлетворяющее начальному условию

(6:2)

Решение задачи имеет следующий вид

(6:3)

где

(6:4)

– функция Грина, которая описывает влияние мгновенного точечного источника,

Формулу (6.3) называют формулой Пуассона.

Выведем формулу Пуассона при n = 1.

(6:5)

(6:6)

Используем метод разделения переменных:

Подставляя в (6:5), получим:

где λ² – параметр разделения, поскольку ‑∞<x<+∞, параметр разделения принимает любые значения. Отсюда следует:

(6:7)

(6:8)

Тогда частные решения уравнения (6:5), удовлетворяющие условию ограниченности, примут вид:

. (6:9)

Поскольку ‑∞<λ<+∞, в (6:9) возьмём знак плюс и образуем функцию

(6:10)

Если производные u_t, u_xx можно вычислять дифференцированием под знаком интеграла (6:10), то функция (6:10) будет удовлетворять уравнению (6:5) как суперпозиция его частных решений.

Требуя выполнения начального условия при t=0, будем иметь:

(6:11)

Воспользуемся формулой обратного преобразования Фурье:

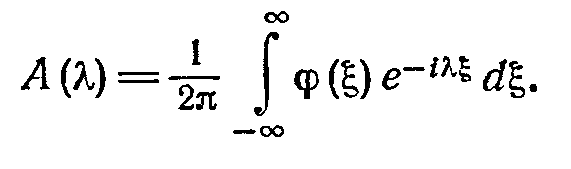(6:12)

Подставляя (6:12) в (6:10) и меняя порядок интегрирования, получим:

(6:13)

Рассмотрим внутренний интеграл в (6:13):

(6:14)

Подставляя (6:14) в (6:13)

(6:15)

Функция Грина имеет вид:

Таким образом, в одномерном случае формула (6.3) принимает вид

и дает решение задачи, например, о распространении тепла в неограниченном стержне.

В ряде случаев решение краевой задачи, построенное с помощью формулы Пуассона, можно преобразовать к виду, содержащему специальную функцию – интеграл ошибок:

и воспользоваться ее свойствами

erf(‑x) = erf(x); erf(∞) = 1.

Пример 1. Найти решение задачи Коши:

u_t = 4u_xx + 8u_x + 3u + e^-x(1 + te^-t); |x| < +∞; t > 0; (A1)

u(x,0) = 2e^-x; |x| < +∞. (A2)

Решение. Нетрудно показать, что с помощью преобразования вида:

u(x,t) = e^-(x+t)v(x,t) (A3)

u_t(x,t) = ‑e^-(x+t)v(x,t) + e^-(x+t)v_t(x,t)

u_x(x,t) = ‑e^-(x+t)v(x,t) + e^-(x+t)v_x(x,t)

u_xx(x,t) = e^-(x+t)v(x,t) ‑e^-(x+t)v_x(x,t) ‑e^-(x+t)v_x(x,t) + e^-(x+t)v_xx(x,t)

‑e^-(x+t)v(x,t) + e^-(x+t)v_t(x,t) = 4e^-(x+t)v(x,t) ‑4e^-(x+t)v_x(x,t) ‑4e^-(x+t)v_x(x,t) + 4e^-(x+t)v_xx(x,t) +

‑8e^-(x+t)v(x,t) + 8e^-(x+t)v_x(x,t) + 3e^-(x+t)v(x,t) + e^-x(1 + te^-t);

e^-tv_t(x,t) = + 4e^-tv_xx(x,t) +1 + te^-t;

e^-xv(x,0) = 2e^-x;

исходная задача (A1)-(A2) сводится к задаче относительно новой неизвестной функции v(x,t) :

v_t = 4v_xx + t + e^t; |x| < +∞; t > 0; (A4)

v(x,0) = 2; |x| < +∞. (A5)

Для ее решения воспользуемся формулой Пуассона, будем иметь

.

Так как

то получим

.

Следовательно, согласно (A3), установим решение задачи (A1)-(A2):