§5. Метод интегральных преобразований

Определение. Интегральным преобразованием (образом) функции f(t) называется

(5:1)

Функция f(t) называется оригиналом своего образа (изображения) F(z); а функция K(z,t) – ядром интегрального преобразования.

Должно существовать обратное преобразование

(5:2)

Интегральное преобразование определено, когда интеграл правой части (5:1) существует. Прямое (5:1) и обратное (5:2) интегральные преобразования устанавливают взаимно – однозначное соответствие между оригиналом и изображением.

Интегральное преобразование над некоторым классом функций f(t) определяется выбором ядра K(z,t) и промежутком интегрирования (a,b). Соответствующим выбором ядра необходимо установить соответствие между уравнениями для оригиналов и уравнениями изображений так чтобы задача для оригинала сводилась к намного более простой задаче для изображения. Часто ядро выбирается так, чтобы дифференциальным операциям над оригиналом соответствовали алгебраические операции над изображением. Ядро K(z,t) выбирается в соответствии с дифференциальным уравнением и граничными условиями задачи.

Когда функция f(t) определена для всех действительных значений t; вводится преобразование Фурье

(5:3)

В случае, когда функция f(t) – непрерывная всюду, кроме, быть может, конечного числа точек разрыва первого рода, для существования преобразования Фурье достаточна абсолютная сходимость интеграла

Оригинал для образа Фурье (5.3) определяется по формуле обращения (обратное преобразование Фурье)

(5:4)

Если f(t) – четная функция, то преобразования Фурье (5.3) и (5.4) переходят во взаимно обратные косинус-преобразования Фурье

;

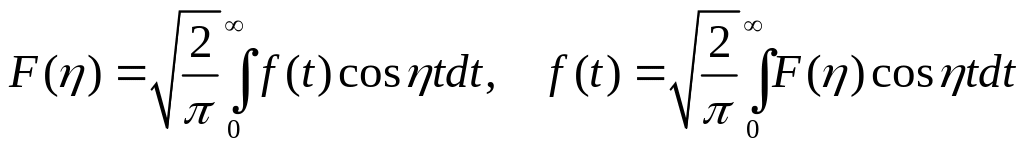а если f(t) – нечетна, то, соответственно, – в синус-преобразования Фурье

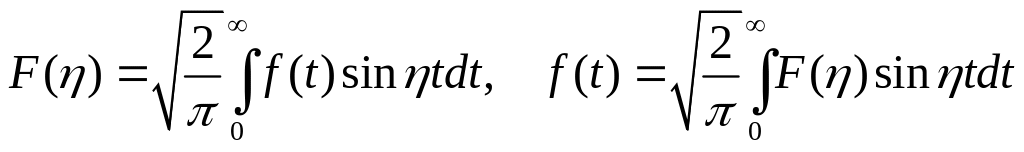
Чтобы решить краевую задачу для функции u(x,t) с помощью интегрального преобразования Фурье, по переменному x переходят к задаче для образа Фурье этой функции U(η,t); находят этот образ. После этого с помощью обратного преобразования Фурье "восстанавливают оригинал". Выбор ядра K(z,t) для задач на полупрямой зависит от вида граничного условия.

Если ; для функции f(x,t) вводится многомерное преобразование Фурье, которое определяется формулами:

где ξ = (ξ₁,…,ξ _n); (x,ξ) = x₁ξ₁+…+x_nξ_n; dx = dx₁ … dx_n; dξ = dξ₁ … dξ_n.

Пример 1. C помощью интегрального преобразования Фурье решить следующую краевую задачу:

u_t = a²u_xx; ‑∞ < x < +∞; t > 0; (A1)

u(x,0) = f(x); ‑∞ < x < +∞. (A2)

Решение. Умножим обе части уравнения (A1) на 1 и проинтегрируем полученное равенство по x на промежутке от ‑∞ до +∞; предполагая, что функция u и ее производная u_x достаточно быстро стремятся к нулю при x → ±∞. Преобразование левой части уравнения (A1) дает:

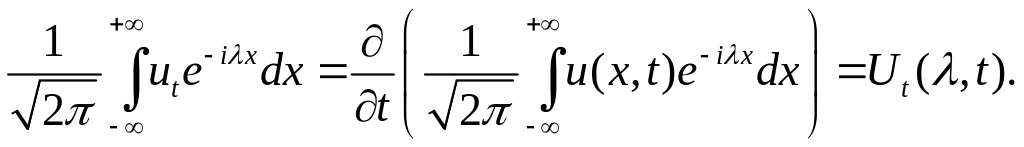
Преобразуем правую часть, применяя правило интегрирования по частям:

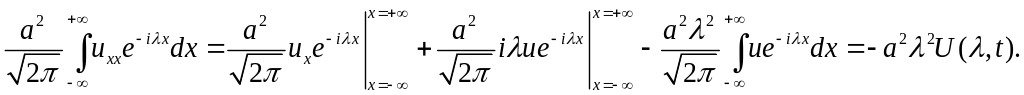
Применив преобразование Фурье к начальным условиям (A2), получим

(A3)

Таким образом, с помощью преобразования Фурье по переменной x :

(A4)

исходную задачу (A1)-(A2) свели к задаче Коши с параметром λ :

(A5)

решением которой является функция:

Для построения решения исходной задачи к полученному выражению для изображения U(λ,t) применим обратное преобразование Фурье. Учитывая формулу (A3), будем иметь:

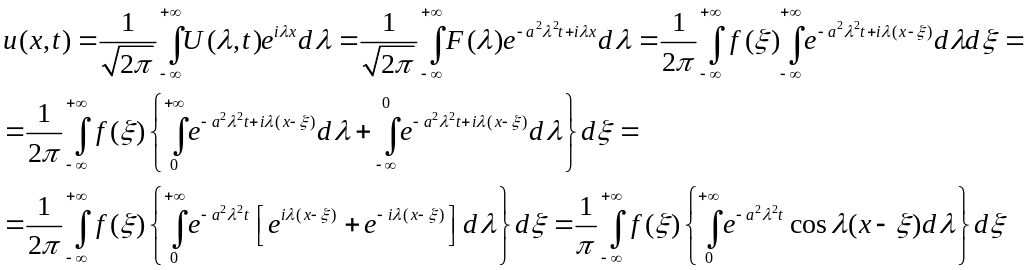
Вычислим интеграл

(A6)

Который сходится при любых значениях параметра x (по признаку Вейерштрасса). Дифференцируя интеграл (A6) по параметру x и применяя правило интегрирования по частям:

получим дифференциальное уравнение относительно I(x):

Решим его:

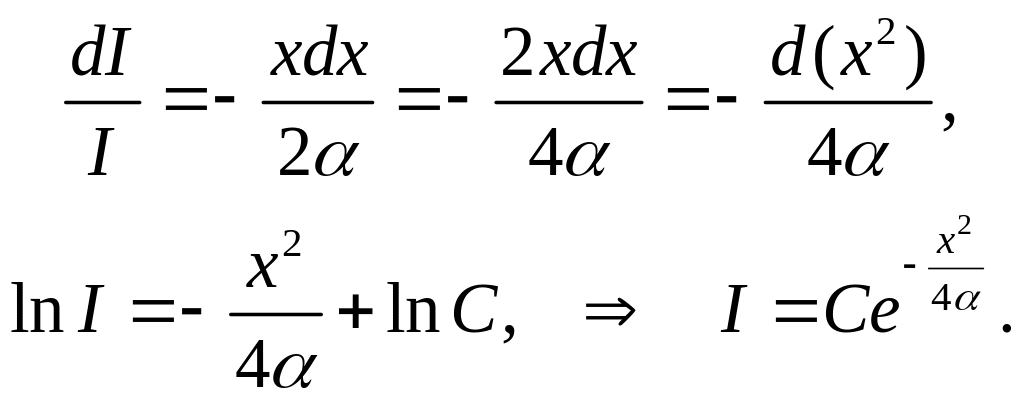
Проверим:

.

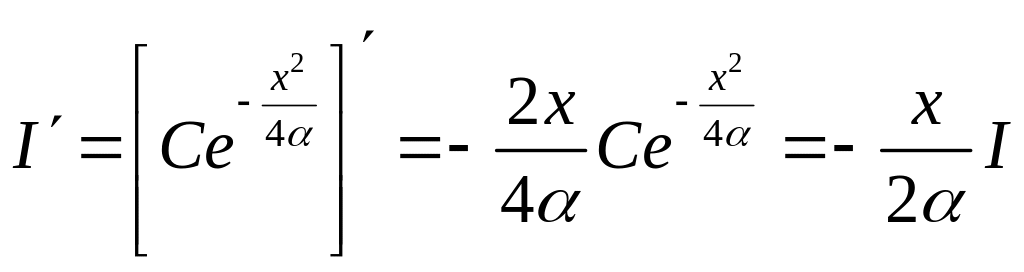Т.о. общее решение имеет вид:

Учитывая равенство

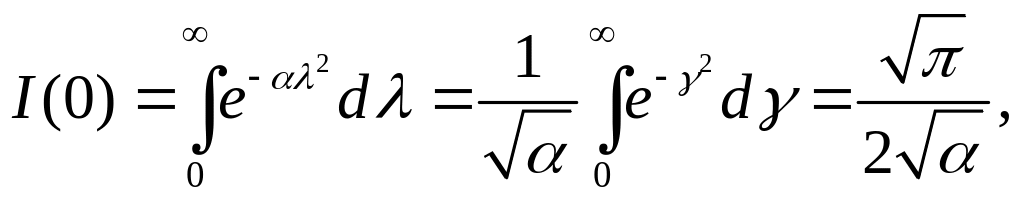
найдём и, следовательно, искомое значение интеграла (A6):

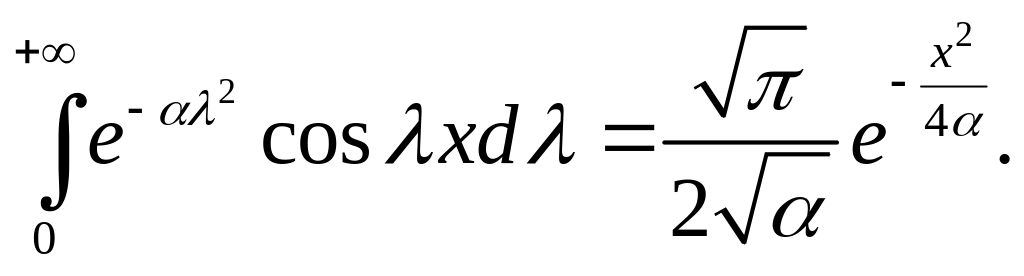
Таким образом, окончательно выражение для решения краевой задачи примет вид:

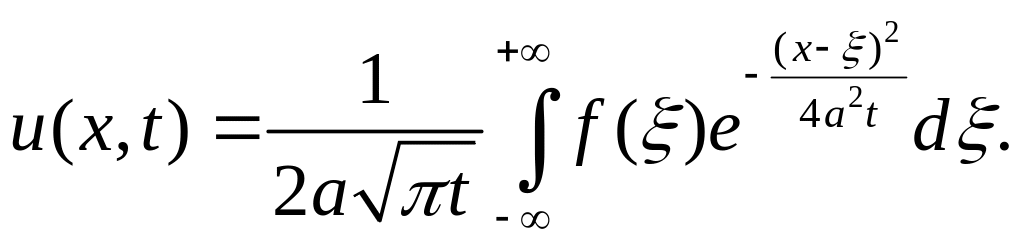
Замечание. В ходе решения задачи была установлена справедливость следующих равенств:

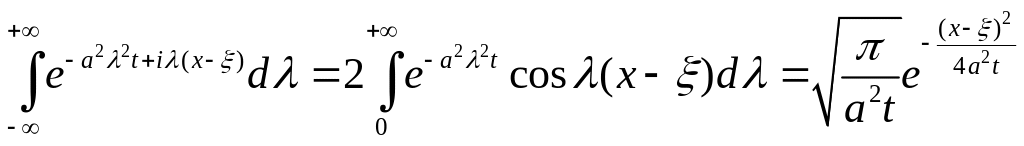(A7)