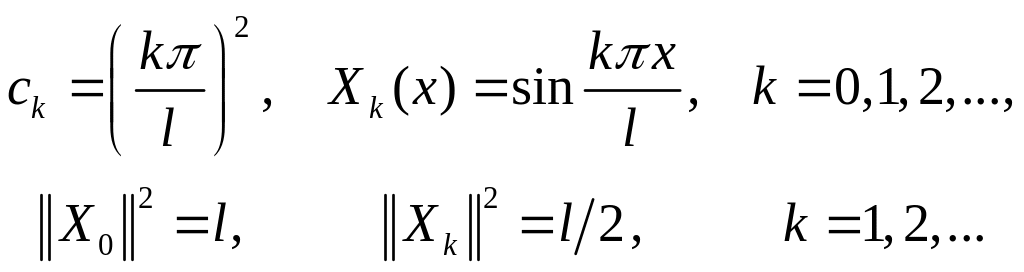§3. Задача Штурма-Лиувилля. Свойства собственных функций
Рассмотрим на промежутке (0,l) для функции X = X(x) обыкновенное дифференциальное уравнение второго порядка с постоянным параметром c вида
(3.1)
с заданными краевыми условиями
(3.2)
(3.3)
Здесь ρ(x), p(x), q(x) – достаточно гладкие вещественные функции, причем p(x) > 0; ρ(x) > 0; q(x) ≥ 0.
Задача Штурма-Лиувилля для уравнения (3.1) формулируется следующим образом: найти множество значений параметра c; при которых уравнение (3.1) имеет ненулевое решение, удовлетворяющее однородным условиям (3.2),(3.3).
Найденные значения параметра c = ck называются собственными значениями задачи Штурма-Лиувилля, а соответствующие им решения Xk(x) задачи (3.1)-(3.3) – собственными функциями.
Свойства решений задачи Штурма-Лиувилля
1. Задача Штурма-Лиувилля (3.1)-(3.3) имеет счетное множество собственных значений c1, c2, … и все они вещественны.
2. Каждому собственному значению ck соответствует единственная (с точностью до постоянного множителя) собственная функция Xk(x):
3. Если функция
(i –мнимая единица)
является собственной, соответствующей
собственному значению
,
то ее вещественная и мнимая части также
являются собственными функциями,
соответствующими тому же значению
.
Собственные функции задачи можно выбрать
вещественными.
4. Собственные функции на отрезке [0; l] образуют ортогональную систему с весом ρ(x):
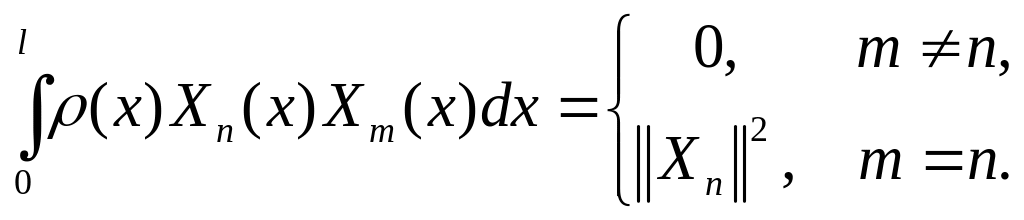
5. Система собственных функций задачи Штурма-Лиувилля полна в пространстве L2(0,l).
6. (Теорема Стеклова.) Всякая функция f(x); удовлетворяющая краевым условиям (3.2)-(3.3) и имеющая непрерывную первую производную и кусочно-непрерывную вторую производную, разлагается в абсолютно и равномерно сходящийся ряд по собственным функциям
В случае когда p(x) ≡ 1; ρ(x) ≡ 1; q(x) ≡ 0; задача Штурма-Лиувилля принимает вид:
X” + c · X(x) = 0; (3.4)
α1X’(0) + β1X(0) = 0; (3.5)
α 2X’(l) + β2X(l) = 0; (3.6)
α2i + β2i = 0; i = 1, 2.
Пусть
– полная ортогональная на [a;b]
система функций, а функция
.
Ряд
где
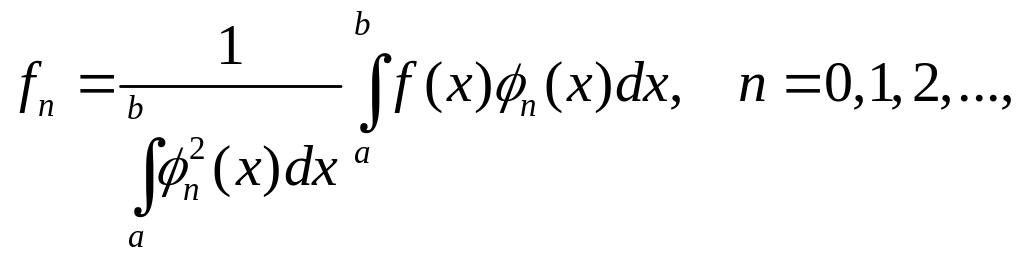
называется ортогональным разложением или рядом Фурье функции f(x) по системе Φ. Числа fn называются коэффициентами Фурье функции f(x) по системе Φ. Интеграл
определяет квадрат нормы функции
.
Пример 1. Найти собственные значения ck и собственные функции Xk(x) следующей задачи Штурма-Лиувилля:
X”(x) + cX(x) = 0; 0 < x < l; (A11)
X’(0) ‑ hX(0) = 0; X(l) = 0; h = const > 0: (A12)
Решение. Прежде всего докажем, что все собственные числа задачи (A1) являются положительными. Действительно, умножив скалярно правую и левую часть уравнения (A11) на функцию X(x); получим:
Откуда, применив к первому слагаемому полученного выражения правило интегрирования по частям и условия задачи (A1+) при x = 0 и x = l; найдем
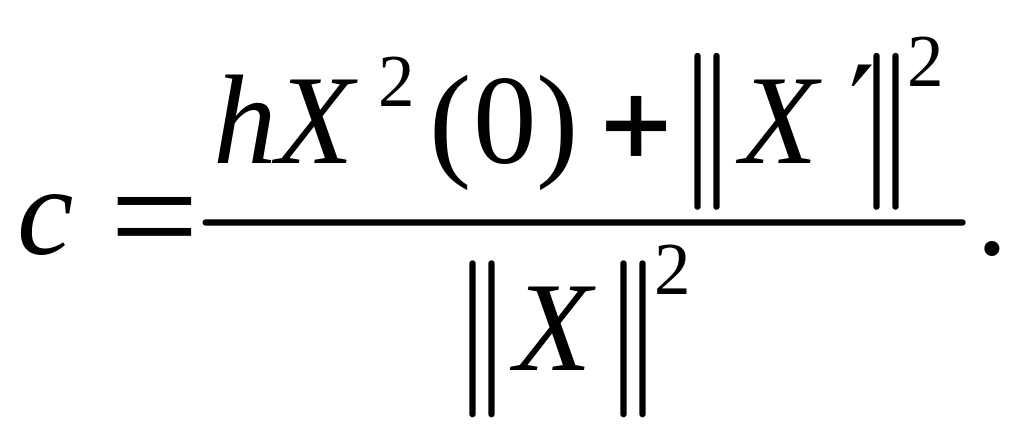(A2)
Отсюда, очевидно, следует неотрицательность значения c. Формула (A2) выражает собственное значение через соответствующую ему собственную функцию.
Покажем, что c ≠ 0: Предположим противное. Пусть среди собственных чисел есть нулевое и ему соответствует ненулевая вещественная собственная функция X(x). Тогда из равенства (A2) при c = 0 следует
X(0) = 0 и ||X’||2 = 0.
Откуда, учитывая свойства нормы функции, можно сделать вывод, что X(x) ≡ 0. А значит, ненулевой функции, соответствующей нулевому собственному значению, нет. Можно показать, что собственной функции вида X = X1 + iX2 с ненулевыми вещественной или мнимой частями, соответствующей собственному значению c = 0; также нет (покажите это самостоятельно).
Таким образом, все собственные значения задачи Штурма-Лиувилля (A1) положительны.
Теперь приступим к построению решения задачи. Ради удобства обозначим c = λ2. Общее решение уравнения (A11) имеет вид:
X(x) = A sin λx + B cos λx. (A3)
Подберем произвольные постоянные A и B и параметр λ так, чтобы удовлетворялись граничные условия (A12): Подстановка выражения (A3) в условия (A12) дает систему линейных уравнений с параметром λ относительно A и B.
(A4)
которая имеет ненулевое решение, если ее определитель равен нулю:
Отсюда получаем уравнение для определения собственных чисел c = λ2:
λ cos λ l + h sin λ l = 0 или tg λ l = ‑ λ/h (A51)
или, полагая λ l = μ, будем иметь:
tg μ = ‑ μ/(hl). (A52)
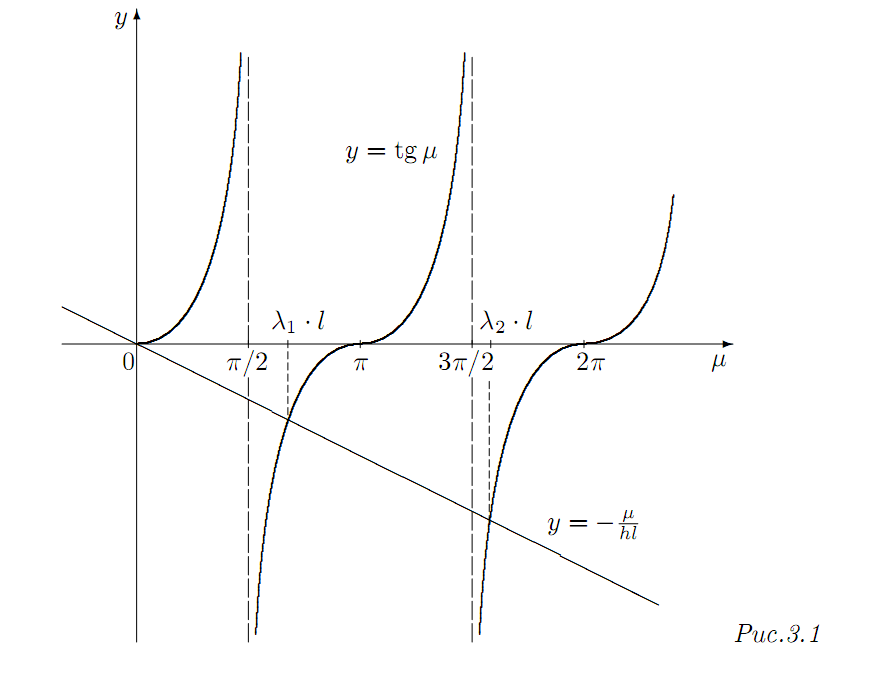
Уравнение (A5) имеет счетное
множество положительных корней
(рис.3.1) (отрицательные корни можно не
рассматривать, так как они новых
положительных собственных значений не
дают). Таким образом, собственные числа
задачи (A1) равны:
ck = λ2k, где λk – положительные корни уравнения (A51). Соответствующие им собственные функции Xk(x); учитывая первое равенство в системе (A4), запишем в виде:
Выбирая Bk = λk, получим окончательное выражение для собственных функций задачи (A1):
(A6)
Найдем квадрат нормы функций Xk(x); k = 1; 2; …, вычислив интеграл:
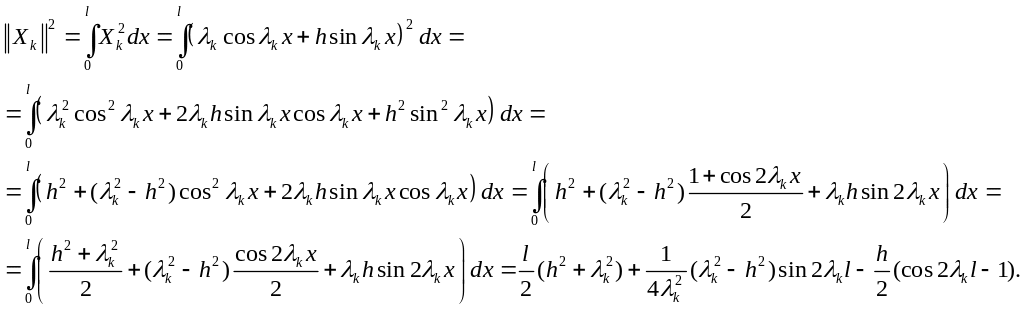(A7)
Так как
и для λ = λ k справедливо равенство (A5) при любом k = 1, 2, …, то путем несложных преобразований выражения (A7) получим следующее выражение для квадрата нормы:
||X||2 = (h + l(λ k2 + h2))/2, k = 1, 2, … .
Можно получить общую формулу, выражающую собственные значения задачи Штурма-Лиувилля (3.4)-(3.6) через соответствующие им собственные функции, в виде:
c = [X’(0)X(0) – X’(l)X(l) + ||X’||2]/||X||2
где связь между величинами X(0), X’(0),X(l) и X’(l) описывают условия (3.5), (3.6).
Простейшие задачи Штурма-Лиувилля для уравнения X” + cX = 0
Вид условия |
Собственные значения и функции |
|
|
|
|
|
|
|
|
Для уравнения (3.4):
X” + c · X(x) = 0;
решите задачу Штурма-Лиувилля при следующих условиях:
а) X(0) = X(l) = 0;
X(x)=Asinλx+Bcosλx;
sinλl=0; λl=kπ; λk=kπ/l; ck=λk2=(kπ/l)2; Xk(x)=sin(kπx/l); k=1,2,…
