Аналитические методы решения краевых задач математической физики

§1. Преобразование краевых задач

В математической физике разработан ряд методов, которые применяются к решению краевых задач определенного вида. На практике часто исходная постановка задачи не позволяет непосредственно применить выбранный метод или воспользоваться известными формулами, определяющими решение (такими, например, как формулы Даламбера и Пуассона). Однако существуют различные приемы преобразования или редукции (сведения) краевых задач к виду, который, возможно, будет удовлетворять условиям применимости того или иного метода решения. Одним из таких приемов является введение новых переменных, с его помощью, например, заданное уравнение можно привести к каноническому виду (см. главу II). Некоторые приемы преобразования задач рассмотрены в примере и предлагаемых упражнениях.

Пример 1. Рассмотрим смешанную задачу: в области 0 < x < l; t > 0 найти решение уравнения

u_tt = a²u_xx + f(x); (A1₁)

удовлетворяющее граничным условиям:

a₁u_x(0, t) + b₁u(0, t) = μ₁;

a₂u_x(l, t) + b₂u(l, t) = μ₂; (A1₂)

a_k; b_k; μ_k ‑ const; a_k² + b_k² ≠ 0; k = 1; 2

и начальным условиям

u(x, 0) = φ(x); u_t(x, 0) = ψ(x); (A1₃)

Покажем, что сформулированная неоднородная задача (A1) может быть приведена к виду однородной смешанной задачи (с однородным уравнением и однородными граничными условиями).

Действительно, пусть функция w = w(x) является решением задачи:

a²w’’(x) = ‑f(x); 0 < x < l;

a₁w’(0) + b₁w(0) = μ₁; (A2)

a₂w’(l) + b₂w(l) = μ₂.

Будем искать решение задачи (A1) в виде:

u(x, t) = v(x, t) + w(x); (A3)

где v(x, t) – неизвестная функция. Подставим выражение (A3) в уравнение (A1₁):

v_tt = a²v_xx + a²w’’(x) + f(x).

Откуда, зная, что w(x) – решение задачи (A2), получим однородное уравнение для функции v :

v_tt = a²v_xx.

Далее подставим выражение (A3) в граничные условия (A1₂):

a₁(v_x(0, t) + w’(0)) + b₁(v(0, t) + w(0)) = μ₁;

a₂(v_x(l, t) + w’(l)) + b₂(v(l, t) + w(l)) = μ₂.

Откуда, учитывая условия задачи (A2) для функции w(x); получим однородные граничные условия для функции v(x, t). Осталось подчинить выражение (A3) начальным условиям (A1₃), чтобы получить начальные условия для функции v :

v(x, 0) = φ(x) ‑ w(x); v_t(x, 0) = ψ(x).

Следовательно, если искать решение задачи (A1) в виде суммы двух функций (A3), одна из которых w(x) является решением задачи (A2), то вторая функция v(x, t) должна быть решением следующей однородной задачи:

v_tt = a²v_xx, 0 < x < l; t > 0;

a₁v_x(0, t) + b₁v(0; t) = 0; (A4)

a₂v_x(l, t) + b₂v(l, t) = 0;

v(x,0) = φ(x) ‑ w(x); v_t(x, 0) = ψ(x).

Таким образом, найдя решение w = w(x) задачи (A2), с помощью преобразования (A3) неоднородная задача (A1) сводится к однородной задаче (A4) относительно новой функции v.

Замечание. Можно показать, что для произвольной функции f(x) условием разрешимости задачи (A2) является выполнение следующего неравенства: a₁b₂ ‑ a₂b₁ ‑ b₁b₂l = 0.

Упражнения

1. Покажите, что задачу

u_xy + au_x + bu_y = 0; u(0, y) = e^‑ay; u(x, 0) = 1;

полагая

u(x, y) = e^‑ay‑bx · v(x, y); ξ = ax, η = by,

можно свести к задаче относительно новой функции v(ξ, η) :

v_ξη = v, v(0,η) = 1; v(ξ,0) = exp(ξb/a).

2. Покажите, что решение задачи

u_tt + 2βu_t + β²u = a²u_xx, 0 < x < l; t > 0;

u(0, t) = u(l, t) = 0; u(x, 0) = φ(x), u_t(x, 0) = ψ(x);

представимо в виде

u = e^‑βtv,

где v(x, t) – решение задачи

v_tt = a²v_xx, 0 < x < l, t > 0;

v(0, t) = v(l, t) = 0; v(x, 0) = φ(x); v_t(x, 0) = ψ(x) + β φ(x).

3. Покажите, что решение задачи

u_tt = a²u_xx + f(x); 0 < x < l, t > 0;

u(0, t) = u(l, t) = 0, u(x, 0) = u_t(x, 0) = 0

представимо в виде u(x, t) = v(x) + w(x, t); где v(x) – решение уравнения

a²v’’(x) + f(x) = 0;

удовлетворяющее однородным краевым условиям v(0) = v(l) = 0; а w(x, t) – решение задачи

w_tt = a²w_xx, 0 < x < l, t > 0;

w(0, t) = w(l, t) = 0; w(x, 0) = ‑v(x); w_t(x, 0) = 0.

4. Пусть v(x, t, τ ) – решение задачи

v(x,τ,τ) = 0; v_t(x,τ,τ) = g(x,τ).

Покажите, что функция

является решением уравнения

u_tt ‑ u_xx = g(x,t);

удовлетворяющим однородным начальным условиям

u(x,0) = ut(x,0) = 0.

5. Редуцировать краевую задачу для уравнения

в прямоугольнике, ограниченном прямыми x = 0; x = π; y = 0; y = T > 0; с условиями

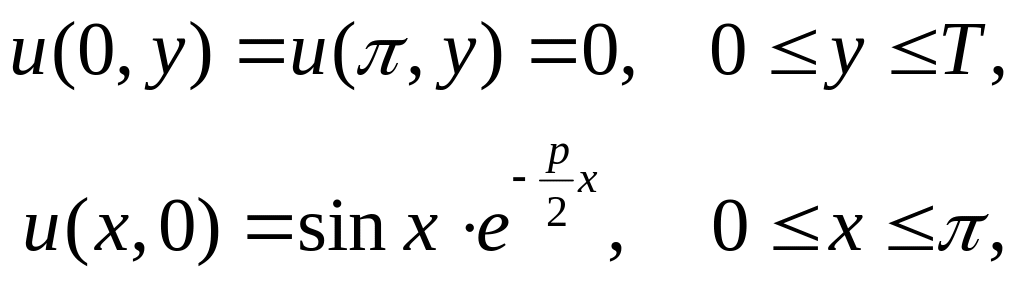
к краевой задаче для уравнения, не содержащего частной производной первого порядка по x и неизвестной функции.

6. Покажите, что функцию, удовлетворяющую условиям:

a₁u_x(0,t) + b₁u(0,t) = μ(t);

a²u_x(l,t) + b₂u(l,t) = ν(t);

a_i² + b_i² = 0; i = 1, 2;

можно искать в виде

u(x,t) = (A₁x² + B₁x + C₁)μ(t) + (A₂x² + B₂x + C₂)ν(t).

7. Приведите примеры функций, удовлетворяющих условиям:

1) u(0,t) = t; u(l,t) = l + t;

2) u_x(0,t) = u(1,t) = t;

3) u(0,t) = μ(t); u(l,t) = ν(t);

4) u_x(0,t) = μ(t); u(l,t) = ν(t);

5) u(0,t) = μ(t); u_x(l,t) = ν(t);

6) u_x(0,t) = μ(t); ux(l,t) = ν(t);

7) u_x(0,t) ‑ hu(0,t) = μ(t); u(l,t) = ν(t);

8) u_x(0,t) ‑ hu(0,t) = μ(t); u_x(l,t) + hu(l,t) = ν(t).

8. Редуцировать первую краевую задачу для уравнения

u_xx ‑ u_t = f(x,t)

в прямоугольнике 0 < t < T; 0 < x < 1 с неоднородными условиями на боковых сторонах

u(0,t) = μ(t); u(1,t) = ν(t); 0 < t < T;

к первой краевой задаче с однородными краевыми условиями на боковых сторонах.

9. Покажите, что решение задачи

u_t = a²u_xx; 0 < x < l; t > 0;

u(x,0) = φ(x); 0 · x · l;

u(0,t) = u₀; u(l,t) = u₁; t ≥ 0; u₀; u₁ ‑ const;

можно искать в виде ; где – стационарная температура стержня, определяемая условиями

а функция v(x,t) – отклонение от стационарной температуры – является решением краевой задачи

v_t = a²v_xx; 0 < x < l; t > 0;

v(0,t) = v(l,t) = 0; t ≥ 0;

10. Покажите, что решение задачи со стационарными неоднородностями

u_tt = a²u_xx + f(x); 0 < x < l; t > 0;

u(x,0) = φ(x); u_t(x,0) = ψ(x); 0 · x · l;

u(0,t) = u₁; u(l,t) = u₂; t ≥ 0; u₁; u₂ ‑ const;

можно искать в виде ; где – стационарное состояние (струны, стержня), определяемое условиями

а функция v(x,t) – отклонение от стационарного состояния – является решением краевой задачи

v_tt = a²v_xx; 0 < x < l; t > 0;

v(0,t) = v(l,t) = 0; t ≥ 0;

v(x,0) = Á(x) ‑ u(x); v_t(x,0) = Ã(x); 0 · x · l.

Замечание. Для задач со стационарными неоднородностями удобнее выделять стационарное решение и искать отклонение от этого решения.

11. Покажите, что решение краевой задачи

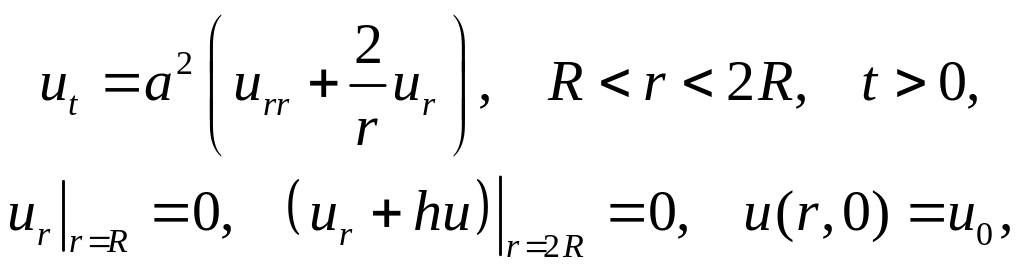
представимо в виде u(r,t) = v/r, где v(r,t) – решение краевой задачи

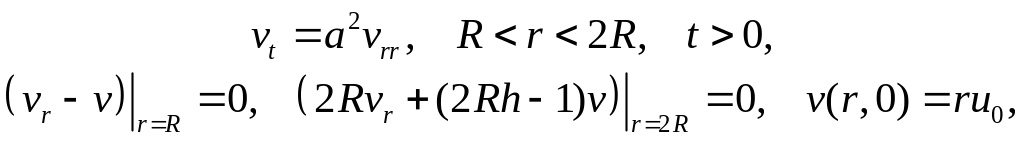
12. Рассмотрим краевую задачу

u_t + u · u_x = a²u_xx, 0 < x < l, t > 0,

u(0,t) = u(l,t) = 0, t ≥ 0;

u(x,0) = f(x); 0 ≤ x ≤ l.

Покажите, если функция v(x,t) является решением задачи

v_t = a²v_xx, 0 < x < l, t > 0,

v_x(0,t) = v_x(l,t) = 0, t ≥ 0,

то функция

u(x,t) = ‑2a²·v_x/v

удовлетворяет уравнению

u_t + u · u_x = a²u_xx.