Доказать тождества:

1. .

2. (AB)C=A(BC).

3. (A\B)(B\A)=(AB)\(AB).

4. (AB)\CA(B\C).

5. .

6. .

7. (((AB)\C)((BC)\A))(AC)AC.

Описать заштрихованные части фигуры как операции над множествами точек плоскости.

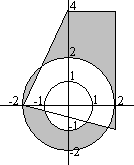
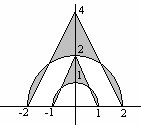
Изобразить графически результат операций над множествами точек плоскости.

1. AB, A={(x,y) : |x|≤y≤4}, B={(x,y) : y≤1/|x| }

2. AΔB, U={(x,y) : y≤3}, A={(x,y) : x²-9≤3y≤ 2-x²}, B={(x,y) : x²-9≤3y≤3/|x| }

3. , U={(x,y) : x²+y²≤9}, A={(x,y) : 4≤ x²+y²≤ 9}, B={(x,y) : y≤1/|x| }

4. (AB)(BC)(AC), A={(x,y) : (x-1)²≤|y|≤ }, B={(x,y) : (x+1)²≤|y|≤ }, C={(x,y) : x²+y²≤4}.

2.2. Отношения на множествах. Бинарные отношения.

При описании числовых множеств на плоскости, мы представляли точку через пару ее координат (x,y) и описывали, например, множество точек внутри окружности как все пары (x,y), удовлетворяющие условию x²+y²≤a². То есть элементы пары связаны между собой некоторым отношением. В данном случае элементами, связанными отношением, являются действительные числа. Но в повседневной жизни мы употребляем это понятие в самых разнообразных контекстах. Например, можно определить отношение между преподавателями и студентами как «A учит B». Ясно, что это отношение будет иметь место не для любой пары «преподаватель – студент», а только для тех, кто преподает и изучает конкретную дисциплину. И ясно, что если мы рассматриваем, кто кого учит, для нас, как и в случае пары координат (x,y), отнюдь не безразлично, в каком порядке записаны элементы пары. Значит, если мы хотим определить такое понятие, как отношение, мы должны, прежде всего, ввести такое понятие, как упорядоченная пара.

Различие между неупорядоченной парой элементов {a,b} и упорядоченной парой (a,b) обычно поясняют на примере сравнения двух пар элементов. Две неупорядоченные пары {a,b}={c,d}, если a=b&c=da=c&b=d. Для упорядоченных пар (a,b)=(c,d)  a=b&c=d. То есть, в общем случае, для упорядоченных пар (a,b)(b,a). Иногда употребляют и такую запись: R=(a,b)={a,{a,b}}. Нетрудно догадаться, что существование множества {a,b} зависит от того, какое мы выберем a. Если a,b – числа, то мы можем описать множество упорядоченных пар в виде графика, откладывая по оси абсцисс значения a, по оси ординат значения b, для которых существует R=(a,b).

Упорядоченную пару R называют двухместным или бинарным отношением. Упорядоченный набор из n элементов (a₁, … , a_n) называют n-местным отношением или кортежем.

Элементы для формирования упорядоченных наборов мы можем выбирать как из одного множества, так и из разных. При построении графиков, которые отображают бинарные отношения между множествами действительных чисел X и Y, мы используем так называемую декартову систему координат. Давайте обобщим эти понятия, поскольку мы уже говорили о том, что элементы упорядоченной пары далеко не всегда бывают числами.

Определение. Прямым (декартовым) произведением двух множеств A и B называется множество упорядоченных пар (a,b), в которых aA и bB:

AB={(a,b)| aA & bB}.

Степенью множества A называется его прямое произведение само на себя:

Aⁿ=A…A – всего n раз.

Нетрудно показать, что |AB|=|A||B| и |Aⁿ|=|A|ⁿ. Попробуйте сделать это сами в качестве упражнения.

Пользуясь введенным понятием прямого произведения, мы можем определить бинарное отношение как подмножество прямого произведения AB:

R=ab={(a,b)R| RAB}.

Обратите внимание, что запись ab обозначает отношение между элементами a и b в общем виде, а запись (a,b) обозначает конкретную упорядоченную пару элементов, то есть один элемент отношения.

Если у нас задан некоторый универсум U, то мы можем рассматривать понятия принадлежности (), включения (), и равенства (=), как отношения на B(U) – множестве всех подмножеств универсума U.

Способы задания отношений. Если отношение содержит небольшое количество пар (или наборов), его можно задать, как и множество, перечислением. Бинарные отношения, как уже говорилось, могут быть заданы в виде графиков, если A,B – числовые множества. В общем случае отношения могут быть заданы в виде таблиц или графов. В реляционных базах данных понятие «кортеж» соответствует записи в таблице, а поля таблицы с именами A,B,C,…, из которых берутся элементы записи, образуют прямое произведение множеств ABC… .

Рассмотрим основные понятия, связанные с понятием бинарного отношения.

Пусть R=ab={(a,b)R| RAB}. Тогда существуют:

обратное отношение R^-1={(b,a)|(a,b)R};

дополнение отношения R={(a,b)|(a,b)R}=(AB)\R;

тождественное отношение I={(a,a)|aA};

однородное отношение: U_R={(a,b)|aA&bA}.

У Новикова [1] однородное отношение называется универсальным отношением. Но чтобы не было путаницы с универсумом, мы будем использовать термин «однородное отношение» для отношения RA², а термин «универсальное отношение» для декартова произведения множеств, на котором задано отношение.

Коль скоро отношения являются множествами упорядоченных пар (или наборов в случае n-местных отношений), то на них можно распространить все операции над множествами и свойства этих операций. Но, кроме них, есть еще одна важная для практических приложений операция над отношениями.

Композиция отношений.

Пусть заданы два бинарных отношения: R₁AB и R₂BC (говорят так: отношение из A в B и отношение из B в C).

Композицией отношений R₁ и R₂ называется отношение R из A в C:

R= R₁ o R₂ ={(a,c)| aA & cC & bB : (a,b)  R₁ & (b,c)  R₂}.

Рассмотрим пример.

Пусть A - множество студентов ФПК, B – множество специальностей, С – множество учебных курсов, изучаемых на этих специальностях. Пусть нам нужно определить, какие дисциплины будет изучать каждый конкретный студент ФПК (что будет включать его приложение к диплому).

Здесь R₁ AB – «студент aA получает специальность bB», R₂ BC – «на специальности bВ изучается дисциплина cC». Искомое отношение R – «студент aA изучает дисциплину cC» есть композиция отношений R= R₁ R₂. То есть, чтобы студент aA изучал дисциплину cC нужно, чтобы он учился на специальности bB, что соответствует отношению ab, и на этой специальности изучалась данная дисциплина cC, что соответствует отношению bc. Значит, для решения задачи нам нужно выяснить, для каких пар (a,b) имеются пары (b,c), и из этих пар составить новые пары (a,c), взяв первый элемент из пары (a,b), а второй элемент – из пары (b,c).

Г рафически операцию композиции можно проиллюстрировать на следующей схеме.

В этой графической схеме каждой упорядоченной паре элементов (a,b) и (b,c) сопоставлены стрелки из множества А в множество B и из множества B в множество C соответственно. Искомым парам (a,c) соответствуют возможные переходы по стрелкам из множества A в множество C.

Теперь составим бинарные таблицы R₁ и R₂ для представленных данной схемой отношений. Элементы этих таблиц r_ij(1) и r_jk(2) соответствуют отношениям (a_i,b_j) и (b_j,c_k). Первая таблица будет содержать |A| строк и |B| столбцов, вторая - |B| строк и |C| столбцов. Для нашего примера таблицы будут иметь вид:

1	0	0
0	1	1
1	0	0
0	1	0

1	0	1	1	0	0
0	1	0	0	1	0
0	0	1	0	0	1

R₁ R₂

Одновременное существование отношений r_ij(1) и r_jk(2) соответствует логическому произведению (конъюнкции) элементов таблицы r_ij(1)  r_ij(2), и значение каждого элемента r_ik итоговой таблицы R будет зависеть от того, принимает ли хотя бы одна из этих элементарных конъюнкций значение «1», что соответствует логическому сложению (дизъюнкции). Для нашего примера r₁₁=(r₁₁₍₁₎ r₂₁₍₁₎ r₃₁₍₁₎ r₄₁₍₁₎ )( r₁₁r₁₂₍₂₎ r₁₃₍₂₎ r₁₄₍₂₎ r₁₅₍₂₎ r₁₆₍₂₎), и так далее. То есть при i=1,…,|A|, j=1,…,|B|, k=1,…,|C| мы имеем: R= R₁ o R₂ = R₁ R₂ , где R₁ R₂ - логическое перемножение матриц.

Степенью отношения Rⁿ называется композиция отношения R n раз с самим собой.

Ядром отношения RAB называется композиция R*= R o R^-1. Ядро отношения является отношением на A.