1.3. Логические законы.
Минимальная дизъюнктивная нормальная форма. Если задача такова, что мы должны оперировать с полным набором двоичных переменных (или с фиксированным числом двоичных разрядов), то мы должны пользоваться СДНФ. Если же нам хочется использовать минимум двоичных переменных и основных операций (например, наиболее просто запрограммировать какое-то сложное логическое условие), лучше воспользоваться самым коротким представлением этой функции в дизъюнктивной или конъюнктивной нормальной форме. Такое представление называют, соответственно, минимальной дизъюнктивной нормальной формой (МДНФ) или минимальной конъюнктивной нормальной формой (МКНФ).
Для сокращения ДНФ мы будем использовать набор простейших тавтологий, которые называют логическими законами. Обычно их рассматривают 8 -10, в зависимости от концепции конкретного автора, но на самом деле часть из них выводима из других.
Закон отрицания отрицания:
.Закон идемпотентности:
.Коммутативность:
.Ассоциативность:
.Дистрибутивность:
.Закон нуля и единицы:
.Законы де Моргана:
.Законы поглощения:
.Законы склеивания:
.
Проверить любой из этих законов можно с помощью таблиц истинности или диаграммы Венна. Теперь же мы займемся получением МДНФ и доказательством более сложных тавтологий с применением логических законов.
Для начала посмотрим, как через дизъюнкцию, конъюнкцию и отрицание выразить остальные операции.
Штрих Шеффера и
стрелка Пирса
представляются через МДНФ согласно
принципу двойственности (закон де
Моргана):
=
,
=
.
Импликация
принимает значение 0 только на наборе
(1,0). СДНФ для нее тогда будет такая:
.
Попробуем получить более короткое
представление. Самый короткий способ
– воспользоваться СДНФ для ее антиоперации
– разности. Она имеет очень простой
вид:
Значит, импликацию можно записать так:
.
Воспользовавшись законом де Моргана,
получаем:
.
Эквивалентность
имеет СДНФ
.
Вряд ли нам удастся получить более
короткое выражение. МДНФ для ее
«антиоперации» – сложения
по модулю 2
- получается через законы де Моргана и
закон нуля и единицы:
.
Рассмотрим, как используются логические законы в преобразованиях логических выражений, на примере доказательства тавтологий.
При выполнении преобразований логических формул часто имеет смысл разбить формулу на части, если это упрощает преобразования.
Пример.
Докажем следующую тавтологию:
В соответствии с
порядком выполнения логических операций
последней будет выполняться импликация
между скобками. Обозначим левую часть
импликации буквой A,
правую – буквой B
и перейдем к ее дизъюнктивной нормальной
форме:
Такой прием позволит нам избавиться от
антидизъюнкции:
Подставив ДНФ для
операции эквивалентности в этом
выражении, перейдем к следующему:
Используем для
преобразования конъюнкции двух отрицаний
закон де Моргана и далее применим
дистрибутивный закон и закон нуля и
единицы:
Теперь займемся
преобразованием правой части исходной
импликации:
В соответствии с
законом поглощения (bc)b=b;
отсюда получаем:
Подставим результаты
преобразований A
и B
в исходное выражение и продолжим
преобразования, выполняя перегруппировку
и используя закон нуля и единицы:
Тавтология доказана.
Упражнения.
1. Используя логические законы и ДНФ логических операций, доказать тавтологии:
1.
;
;
.
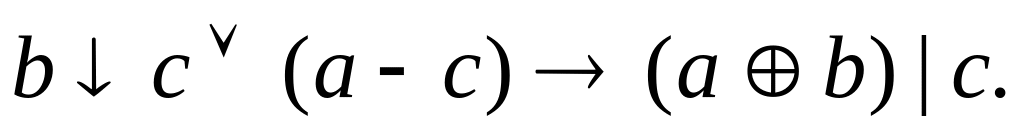
2. Используя логические законы и ДНФ логических операций, найти МДНФ для логических формул:
1.
;
;
;
.
