3.8. Двудольные графы. Паросочетания.

Рассмотрим задачу о назначениях на работу. Пусть имеется n вакансий и m претендентов на эти вакансии, каждый из которых может выполнять определенное количество работ. Для определенности пусть m>n, иначе мы все вакансии ни при каких условиях не заполним.

Рассмотрим граф G, который отображает такую ситуацию (рис.3.12). Обозначим множество кандидатов – V₂, |V₂|=m, множество вакансий – V₁, |V₁|=n. Ребро e=(v_i,v_j) , v_iV₁, v_jV₂ означает, что кандидат v_j по своей квалификации может претендовать на вакансию v_i.

Определение. Граф G называется двудольным, если существуют подмножества V₁,V₂, V₁V₂=, V₁V₂=V, и ребро e=(v_i,v_j) существует, только если v_iV₁, v_jV₂. То есть концевыми вершинами ребра обязательно являются представители разных множеств.

Мы уже упоминали такую конструкцию, когда говорили об операции соединения графов. Она получается в результате соединения двух нуль-графов. Но там был полный двудольный граф, который мы обозначали K_m,n. Произвольный двудольный граф обозначается G(V₁,V₂,E).

Двудольные графы обладают одним важным свойством, которое нам еще понадобится в будущем.

Теорема. В двудольном графе все циклы имеют четную длину.

Доказательство очень простое. Если мы начинаем обход цикла из одной доли и заканчиваем в ней, а ребер внутри доли нет, то каждый переход между вершинами одной доли требует выхода в другую долю и возвращения в исходную. То есть для каждого перехода нужна пара ребер, что и означает четность цикла.

Для графа, содержащего циклы, четность всех циклов – необходимое и достаточное условие его «двудольности». Про графы без циклов – деревья - мы поговорим отдельно.

Теперь введем еще одно определение, касающееся задачи о назначениях на работу.

Определение. Паросочетанием (или независимым множеством ребер) называется такое подмножество E’E, в котором никакие два ребра не смежны. Совершенным паросочетанием из V₂ в V₁ называется паросочетание, покрывающее все вершины из V₁ (в общем случае все вершины минимального из пары множеств V₁,V₂).

Задачу о назначениях на работу тогда можно поставить так: существует ли совершенное паросочетание из V₂ в V₁?

Ответ на этот вопрос дает теорема Холла.

Сначала введем еще одно необходимое понятие.

Определение. Множество вершин, смежных с вершиной v_i, называется множеством смежности этой вершины и обозначается Г⁺(v_i). Если множество смежности включает и саму вершину vi, то его обзначают Г(v_i)= Г⁺(v_i){v_i}. Для некоторого подмножества вершин A множеством смежности Г(А) будет объединение Г⁺(v_i) по всем v_iA.

Теорема Холла. Пусть G(V₁,V₂,E) – двудольный граф. Совершенное паросочетание из V₂ в V₁ существует тогда и только тогда, когда  AV₁ |A||Г(A)|.

Доказательство. Необходимость очевидна. Если совершенное паросочетание существует, то, по самому определению такового, каждая вершина из V₁ связана, как минимум, с одной вершиной из V₂. , и любое их объединение дает требуемое соотношение |A||Г(A)|.

Достаточность. Пусть теперь известно, что |A||Г(A)|. Это означает, что каждая вершина из V₁ связана хотя бы с одной вершиной из V₂, так как множество A может состоять и из одной вершины. Покажем теперь, что в этом случае существует совершенное паросочетание из V₂ в V_{1 .}

. Сделаем дополнительное построение. Стянем вершины из V₁ к вершине u, а вершины из V₂ – к вершине v. Рассмотрим все пути между вершинами u и v. Ясно, что если каждая вершина из V₁ связана хотя бы с одной вершиной из V₂, то через нее проходит какая-то цепь S(u,v). Но нас интересуют только несмежные ребра, следовательно, вершинно непересекающиеся простые цепи. Максимальное число таких цепей по теореме Менгера равно мощности минимального разделяющего множества вершин. По построению V₁ является для u и v разделяющим множеством вершин. Покажем теперь, что оно является минимальным. Если бы это было не так, то существовала бы цепь S’, проходящая мимо множества V₁ (рис.3.13), что противоречит нашему исходному построению.

Значит, V₁ минимально. Итак, мы имеем | V₁| вершинно непересекающихся простых цепей, каждая из которых проходит через какое-то из ребер множества E, причем это ребро не имеет смежных ребер. Это и означает существование совершенного паросочетания.

В качестве примера на применение теоремы Холла выясним, существует ли совершенное паросочетание в следующем двудольном графе:

1) 6,7; 2) 6,7; 3) 6,7; 4) 6,7,8,9; 5) 8,9,10; 6) 1,3,4; 7)1,2,3,4; 8) 4,5; 9) 4,5; 10) 5 .

Д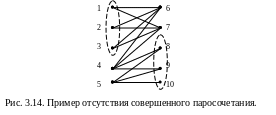 иаграмма этого графа будет выглядеть так, как показано на рис. 3.14. Вершины 1-5 отнесем к множеству V₁, вершины 6-7 к множеству V₂. По условию теоремы для существования совершенного паросочетания любая комбинация вершин из множества V₁ должна быть связана с не меньшим количеством вершин из множества V₂. В данном случае это не выполняется для вершин{1,2,3} из V₁. То есть совершенного паросочетания из V₁ в V₂ не существует. Аналогично можно убедиться, что не существует совершенного паросочетания и из V₂ в V₁, рассмотрев подмножество {8,9,10} из множества V₂.

Упражнения.

Есть ли среди графов, заданных следующими списками смежности, двудольные? Объясните решение.

1. 1) 2,5,8; 2) 1,3,6; 3) 2,4,7; 4) 3,5,8; 5) 1,4,6; 6) 2,5,7; 7) 3,6,8; 8) 1,4,7.

2. 1) 2,6,8; 2) 1,3,5; 3) 2,4,8; 4) 3,5,7; 5) 2,4,6; 6) 1,5,7; 7) 4,6,8; 8) 1,3,7.

3. 1) 2,4,8; 2) 1,3,5,7; 3) 2,4,6,8; 4) 1,3,5,7; 5) 2,4,6,8; 6) 3,5,7; 7) 2,4,6,8; 8) 1,3,5,7.

Проверьте существование совершенного паросочетания для следующих двудольных графов, заданных списком смежности множества V₁.

1. 1) 7,9; 2) 7,8,9; 3) 7,8; 4) 9,10,11; 5) 10,12; 6) 11,12.

2. 1) 7,8; 2)7,9; 3) 8,10; 4) 9,11; 5) 10,12; 6) 11.

3. 1) 7,8; 2) 7,8; 3) 7,8,10; 4) 8,10; 5) 9,10,11; 6) 10,12.