Билет №1: Множества и комбинаторика Множество – объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью. Объекты, которые образуют множество, называют элементами множества, обозначаются латинскими буквами. Множество, содержащее конечное число элементов, называются конечным. Если же множество не содержит ни одного элемента, то оно называется пустым и обозначается . Задание множеств: 1) перечисление элементов ( конечные множества) 2)указание их свойств ( { } ) Множество М` называется подмножеством множества М (М` включено в М) тогда и только тогда, когда любой элемент множества М` принадлежит множеству М: М’ М↔(m ϵ M’→m ϵ M) или М’ М↔(M’={m_j/m_j ϵ M}) Для каждого множества М существует множество, элементами которого является подмножество множества М, и только они. Такое множество будем называть Семейством множества М или булеаном этого множества и обозначать B(М), а множество М будем называть универсальным универсумом или пространством и обозначать единицей. Комбинаторика – раздел дискретной математики посвященный решению задач выбора и расположения элементов некоторого, как правило, конечного множества соответствия с заданными свойствами.

Комбинаторная конфигурация – способ построения некоторой конструкции из элементов множества. Комбинаторными конфигурациями являются: размещение, перестановка, сочетание. Размещение А (n, K) мощности К из n элементов (К≤n) это любая последовательность попарно размещенных К элементов, взятых из N элементов. | А(n,K) |=n*(n-1)…(n-K+1)= Важен состав элементов и их порядок. Перестановка P(n) – размещение при К= n. Число перестановок - | P(n) |из n элементов есть: =n*(n-1)…2*1=n!.. Сочетание C (n, К) мощности К из n элементов называется любое подмножество содержащее К элементов, набранных из n элементов. Важен состав элементов, но порядок роли не играет. |C (n, K)|= = 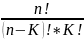Это число равно К-му коэффициенту в разложении бинома Ньютона (a+b) ^n.

Билет №2: Системы счисления. Перевод чисел из одной системы счисления в другую. Системы счисления (нумерацией) называется совокупность приемов и правил для обозначения и наименования чисел количественных эквивалент, позволяющие для каждого числа однозначно получать его кодовую запись и по каждой кодовой записи - соответствующий ей количественный эквивалент. Цифры счисления множества элементарных знаков, использованных для кодирования. Системы счисления бывают непозиционными и позиционными. В непозиционных системах каждой цифре сопоставлен некоторый стандартный количественный эквивалент, а количественный эквивалент кода числа вычисляется как некоторая функция от количества эквивалентных цифр, входящих в запись этого кода. В позиционных системах каждой цифре некоторый количественный эквивалент сопоставляется не однозначно, а в зависимости от её положения в коде числа. В зависимости от функции F системы счисления бывает: 1)аддитивные 2) мультипликативные Виды систем счисления. 1) Системы счисления с основание S (Если для любого А и любого i имеет место равенство ϕ(a_j;j)= *ϕ(a_j,,0) 2) Весомозначного типа Если ϕ (a_j; j)= p_i *ϕ (a_j,, 0) и P_i не совпадает при различных j 3) Естественные системы счисления (Если в системе с основание S множество цифр состоит из 0,1…,S-1, то система имеет естественное множество цифр. 4) Симметричная система счисления (Если S=m+k+1 и множество цифр {-m,-m+1,…,-1,0,1,2,…,k}, то при m=k система имеет симметричное множество цифр) 5) Ассиметричная система счисления: (При k>m или m>k система имеет асимметрическое соответственно в положительную или отрицательную сторону множество цифр).

Билет №3 Множества. Операции над множествами. Бинарные отношения. Способы их задания. Множества* (первая часть 1-го билета). Операции над множествами: 1)Объединение M_a∪M_b двух множеств M_a и M_b является множество M₁ состоящее из элементов множества M_a и из элементов множества M_b M=M_a∪M_b={m_i/m_i ∈M_a и m_i∈M_b} 2)Пересечением Ma∩M_b двух множеств M_a и M_b является множество M₁ состоящее из элементов, которые принадлежат как множеству M_a , так и множеству M_b: M=M_a∩M_b= {m_j/m_j ∈M_a и m_i∈M_b} 3) Разностью M_a/M_b двух множеств M_a иM_b является множество M₁ состоящее из элементов, которые принадлежат множеству M_a, и не принадлежащих множеству M_b: M=M_a/M_b={m_j/m_j ∈M_a и m_i ∉M_b} Эти операции являются двуместными. 4) Операция "Дополнения" является одномерной. Дополнением M множества M является множество: M= {m_j/ m_j ∉M} Множество можно задать выражением, в которое входят идентификаторы (указатели) множеств, операции и, быть может, скобки. такой способ задания называется аналитическим. Бинарным отношением T во множестве M называется подмножество его квадрата: T⊂M². Поэтому говорят, что элементы m_i и m_j , находятся в отношении T, если (m_i, m_j) ∈T. Совокупность множеств M с заданными в нем бинарным отношением T⊂M² называется графом G: G<M,T>, где M - носитель графа T - сигнатура графа. Способы задания бинарных отношений: 1)При математическом задании используют двумерную таблицу - матрицу смежности, каждой строке (столбцу) которой взаимно однозначно составляют элемент множества M. Тогда каждая клетка (i, j) взаимно однозначно соответствует элементам множества M². Клетку (i, j), которая соответствует элементу, принадлежащему T⊂M^2, каким либо образом помечают, например, зачерняют или помещают в нее 1; остальные клетки оставляют незачеркнутыми или в них записывают нули.

M={ a,b,c,d,e} 0 1 1 1 0 a 0 0 1 1 1 b B= 1 1 0 1 1 c 0 1 1 0 1 d 0 0 1 0 0 e 2) Задание бинарного отношения с помощью фактормножества. Окрестностью единственного радиуса элемента m_i∉M называется множество элементов m_j∉M таких, что (m_i, m_j) ∈T, T⊂M². Часто вместо термина окрестность единственного радиуса используют термин сечение. Множество окрестностей единственного радиуса, взятых для всех элементов множества M при задании в нём отношения T⊂M² , называется фактормножеством M/T множества M по отношению T. Фактормножество M/T полностью определяет отношение T. Например: a b c d e [{b,c,d} {c,d,e} {a,b,d.e} {b,c,e} {c}] Бинарное отношение, задается графом G=<M,T>, можно задать и перечислением его дуг: M={a,b,c,d,e}, T={(a,b), (a,c), (a,d), (d,c), (b,c), (b,e), (b,d), (c,a), (c,b), (c,d), (c,e), (d,c), (d,b), (d,e), (e,c)}

Билет №4:Функции. Операция.

Подмножество F⊂My*Mx называется функцией, если для одного элемента x∈Mx найдется не более одного элемента y∈My, вида (х, у) ∈F, при этом функция называется всюду (полностью =) определенной; в противном случае функция называется частично определенной (неопределенной)

Множество Мх образует область определения функции F, множество Му – область значений функции F.

Кол-во аргументов определяет местность функции.

n-местная функция – когда множество Мх в определении функции у = F(x) яв-ся декартовым произведением множеств M_x1, M_x2,…, M_xn,

y = F(x1, x2, .., xn)

Частичный случай n-местной функции y = F(x1, x2, xn) является n-местной операцией.

n-местной операцией On в множестве М понимается n-местная функция y = F(x1, x2, .., xn), у которой области определения аргументов и область значений функции совпадает

M = Mx1 = Mx2 = …=Mxn = My

Таким образом, n-местная операция по n-элементам множества M определяет (n+1)- й элемент этого же множества.

Имеются 4 операции над множествами(3 билет)

Операции над множествами: 1)Объединение M_a∪M_b двух множеств M_a и M_b является множество M₁ состоящее из элементов множества M_a и из элементов множества M_b M=M_a∪M_b={m_i/m_i ∈M_a и m_i∈M_b} 2)Пересечением Ma∩M_b двух множеств M_a и M_b является множество M₁ состоящее из элементов, которые принадлежат как множеству M_a , так и множеству M_b: M=M_a∩M_b={m_j/m_j ∈M_a и m_i∈M_b} 3) Разностью M_a/M_b двух множеств M_a иM_b является множество M₁ состоящее из элементов, которые принадлежат множеству M_a, и не принадлежащих множеству M_b: M=M_a/M_b={m_j/m_j ∈M_a и m_i ∉M_b} Эти операции являются двуместными. 4) Операция "Дополнения" является одномерной. Дополнением M множества M является множество: M= {m_j/ m_j ∉M} Множество можно задать выражением, в которое входят идентификаторы (указатели) множеств, операции и, быть может, скобки. такой способ задания называется аналитическим.

5)Фундаментальные алгебры

Алгебра А - совокупность множества М с заданными в нем операциями

S={f₁₁,f₁₂,…,f_1n1,f₂₁,f₂₂,…,f_2n2,…,f_m1,f_m2,…,f_mnm} (обозначается А=<M,S>) , где первый индекс идентификатора операции указывает на размерность.

Рассмотрим фундаментальные алгебры.

Алгебра вида <M,f₂> -группоид. Если f₂ –операция типа умножения, то группоид мультипликативный, если f₂ – операция типа сложения, то группоид аддитивный.

Пусть А=<M,f₂> - группоид. Обозначим f₂ как о, тогда элемент е, принадлежащий М, называется правым нейтральным элементом группоида А, если для любого м, принадлежащего М, выполняется м о е = м, и левым нейтральным элементом группоида А , если е о м = м.

Если е, принадлежащий М, группоида А=<M,o> - и левый, и правый нейтральный элемент группоида А, то его называют двустронним нейтральным элементом (или нейтральным элементом). Никакой группоид не может иметь более одного нейтрального элемента. Если группоид А=<M,o> мультипликативный, то нейтральный элемент называется единицей и обозначается 1. Если группоид аддитивный, то нейтральный элемент – нуль и обозначается 0.

Группоид А – иденпотентный, если его сигнатура удовлетворяет закону иденпотентности: для любого м, принадлежащего М, выполняется м о м = м.

Группоид А – коммутативный (абелевый), если его сигнатура удовлетворяет закону коммутативности: : для любых х и у, принадлежащих М, выполняется х о у = у о х.

Группоид А – ассоциативный (полугруппа), если его сигнатура удовлетворяет закону ассоциативности: : для любых х, у и z, принадлежащих М, выполняется

х о (у о z) = (х о у) о z.

Полугруппа <М,о>, в которой обратные операции(то есть для любых а и b, принадлежащих М, каждое из уравнений а о х = b, у о а = b) обладают единственным решением , называется группой.

Алгебра <М,*,+>, в которой умножение связано со сложением законами дистрибутивности (а*(b+с)=а*b+b*с, (b+с)*a=b*а+с*а), называется кольцом.

Кольцо, в котором все отличные от нуля элементы составляют группу по уножению, называется телом. Тело, у которого мультипликативная группа абелева, называется полем.

Билет №6:Алгебра Кантора, Законы алгебры Кантора.

Алгебра множеств (алгебра Кантора, алгебра классов)

Ак=<B(1), ∪,∩, ->, носителем которой является булеан универсального множества 1, сигнатурой - операции объединения U, пересечения ∩ и дополнения

Законы алгебры Кантора

1. Закон коммуникативности, объединения и пересечения:

Ma∪Mв = Мв∪Ма, Ма∩Мв = Мв∩Ма;

2. Закон ассоциативности, объединения и пересечения

Ma∪( Мв∪Мс) = (Ma∪Mв) ∪Мс;

Ma∪( Мв∩Мс) = (Ma∩Mв) ∩Мс;

3. Закон дистрибутивности, пересечения относительно объединения и объединения относительно пересечения:

Ма ∩(Мв∪Мс) = Ма∩Мв∪Ма∩Мс;

Ma∪Мв∩Мс = (Ma∪Mв) ∩ (Ма∪Мс);

4. Закон поглощения:

Ма∪Ма∩Мв = Ма, Ма ∩(Ма∪Мв)= Ма;

5. Закон сохранения

Ма∩Мв∪Ма∩ = Ма,

(Ма∪Мв) ∩(Ма∪ ) = Ма;

6. Законы Порецкого

Ма∪ ∩Мв = Ма∪Мв;

Ма∩( ∪Мв) = Ма∩Мв;

7. Закон идемпотентности объединения и пересечения

Ма∪Ма = Ма

Ма∩Ма=Ма

8. Закон действия с универсальным (1) и пустым множествами:

М∪ = М, М∩ = , М∪1 = 1;

М∩1 = М, М∪ = 1, М ∩ = ;

9. Закон де Моргана

10. Закон двойного дополнения

= М.