
29. Скорость и ускорение точки в полярных координатах
Рассмотрим, как
вычисляются скорость и ускорение точки
при задании ее движения в полярных
координатах, то есть когда заданы
уравнения движения точки в виде r = r(t);
![]() =
(t).
=
(t).
В этом случае векторы v и a определяются по их проекциям на взаимно перпендикулярные подвижные оси Pr , имеющие начало в точке Р и движущиеся вместе с нею (см.рис.). Эти оси направлены следующим образом:
ось Pr направлена по радиусу-вектору точки в направлении от полюса О к точки Р;
ось P получается путем поворота вокруг точки Р оси Pr на прямой угол в положительном направлении отсчета угла , то есть против хода часовой стрелки.
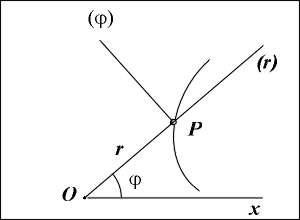
Определение скорости точки
Вектор скорости v
точки направлен по касательной к
траектории и определяется своими
проекциями vr и
![]() на оси Pr и P
по формулам: vr = dr/dt
=
на оси Pr и P
по формулам: vr = dr/dt
=![]() ;
= r(d
/dt) = r
;
= r(d
/dt) = r![]() .
.
Величины vr и соответсвенно называются радиальной и трансверсальной скоростями точки.
В зависимости от знаков производных и радиальная и трансверсальная скорости могут быть как положительными, так и отрицательными (на рисунке показан случай, когда обе эти скорости положительные). Модуль скорости v = ( vr2 + 2 ) 1/2.

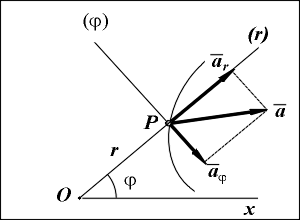
Определение ускорения точки
Вектор ускорения a
точки направлен в сторону вогнутости
траектории и определяется своими
проекциями ar и
![]() на оси Pr и P
по формулам: ar = d2r/dt2
- r (d
/dt)2
=
на оси Pr и P
по формулам: ar = d2r/dt2
- r (d
/dt)2
=![]() - r (
)2;
- r (
)2;
= r (d2
/dt2)
+ 2 (dr/dt) (d
/dt)
= r![]() + 2
.
+ 2
.
Величины ar и соответсвенно называются радиальным и трансверсальным ускорениями точки.
Радиальное и трансверсальное ускорения могут быть как положительными, так и отрицательными (на рисунке показан случай, когда радиальное ускорение положительное, а трансверсальное - отрицательное). Модуль ускорения a = ( ar2 + 2 )1/2 .
30. Поступательное движение
Поступательное движение – это движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе. На рисунках 2.1,а и 2.1,б приведены примеры поступательного движения: движение прямоугольника в плоскости чертежа, движение каждой кабины колеса обозрения.
![]() а
а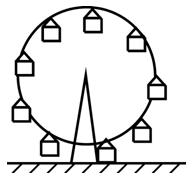 б
б 2.2
2.2
Исходя из определения
поступательного движения, движение
твердого тела может быть задано в
векторном виде формулой (рисунок 2.2):
rM=rA +
AM. В этой формуле AM
- вектор постоянный по величине
и направлению, поэтому производная от
него равна нулю. Для скорости и ускорения
произвольной точки M
получим: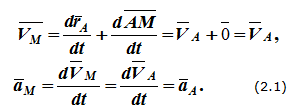
То есть скорости и ускорения точек твердого тела при поступательном движении равны и одинаково направлены, а траектории при наложении совпадают.Для определения кинематических характеристик точек тела достаточно знать закон движения одной из них.
