119 LIij iy-

Table.5 Fuzzified historical enrollments and forecasts of the models ⁽ⁿ⁼¹⁴⁾

Year	Actual enrollment	Forecasts 1-order	Forecasts 2-order	Forecasts 3-order	Forecasts 4-order
1971	13055
1972	13563	13750
1973	13867	14250	13750
1974	14696	14250	14750	14750
1975	15460	15250	15250	15250	15250
1976	15311	15500	15250	15250	15250
1977	15603	15500	15500	15750	15750
1978	15861	16250	16250	16250	15750
1979	16807	16250	16250	16250	16750
1980	16919	17083	17500	16750	16750
1981	16388	17083	16250	16250	16250
1982	15433	15250	15250	15250	15250
1983	15497	15500	15250	15250	15250
1984	15145	15500	15500	15250	15250
1985	15163	15500	15500	15500	15250
1986	15984	15500	15500	15500	15750
1987	16859	16250	16250	16250	16250
1988	18150	17083	17500	17500	17500
1989	18970	18750	18750	18750	18750
1990	19328	19250	19250	19250	19250
1991	19337	19000	19250	19250	19250
1992	18876	19000	18750	18750	18750

355

Table.6 Fuzzified historical enrollments and forecasts of the models ⁽ⁿ⁼²⁸⁾

Year	Actual enrollment	Forecasts 1-order	Forecasts 2-order	Forecasts 3-order	Forecasts 4-order
1971	13055
1972	13563	13625
1973	13867	13875	13875
1974	14696	14625	14625	14625
1975	15460	15375	15375	15375	15375
1976	15311	15375	15375	15375	15375
1977	15603	15375	15375	15625	15625
1978	15861	15875	15875	15875	15875
1979	16807	16875	16875	16875	16875
1980	16919	17125	17500	16875	16875
1981	16388	17125	16375	16375	16375
1982	15433	15375	15375	15375	15375
1983	15497	15375	15375	15375	15375
1984	15145	15375	15375	15125	15125
1985	15163	15500	15500	15500	15125
1986	15984	15500	15875	15875	15875
1987	16859	16875	16875	16875	16875
1988	18150	17125	17500	17500	18125
1989	18970	18875	18875	18875	18875
1990	19328	19375	19375	19375	19375
1991	19337	19125	19375	19375	19375
1992	18876	19125	18875	18875	18875

The implementation using the proposed method shows that the essence of high- order time series models can be obtained while the simplicity of first-order calculation is retained. Comparisons of the results for the first-order model and those of high-order models are made as following.

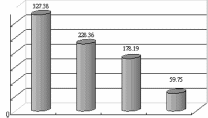
Due to there are no evidences and any implementation to confirm the advantages of the high-order model in the literature, the same example of the historical enrollments in the University Alabama shown in Song and Chissom (1993, 1994) are analyzed using four different models ^(include the ^{first-order, second-order, third-order,} fourth-order ^models) with different numbers of partition n ^(n=7,14 and ^28). In figures ^1-3, the RMS error obtained from results of the first-order, the ^{second-order,} the third-order or the

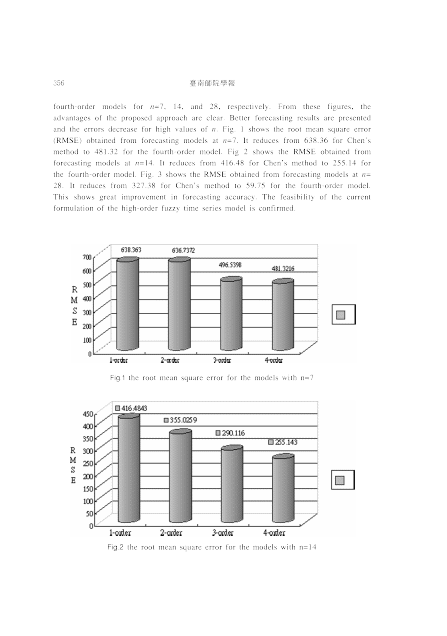
357

300

_R 250

^M 200

E 150

100

50

1-aider 2-crder 3-order 4-aMer

Fig.3 the root mean square error for the models with n=28

2. Song- Chissom method ^/high-order model ^(a new scheme embedded into Song­ Chissom ^method)

^Next, forecasting enrollments are also carried out with Song-Chissom method and another proposed high-order method. The procedure follows:

1. Define the universes of discourse on which the fuzzy sets will be defined.

^{Usually, the minimum value} Xmjn ^{and the maximum value} _Xmax ^{are found and used to define the universe of discourse U. In this case,} Xmjn =13000 ^and _Xmax

=20000. For simplicity, the universe is chosen to be the interval of U=[ 13000,20000].

2. Determine the number of fuzzy partition.

For example, if we take partitions n=7 then the universe is segmented into seven intervals with equal range. Let _{u1, u2, u3, u4, u5, u5} and _u7 denote the seven

intervals.

3. Define fuzzy set on the universe U.

Ai would be the linguistic variable of records of ^enrollments, which is ^{corresponding to each} u,

4. Transfer the historical data into fuzzy set.

In this step, the equivalent fuzzy set to every year’s record is found. The membership of each record to _A will be determined, which can be interpreted as

the degree of each record belonging to each _A.

5. Setup the fuzzy relations based on historical knowledge.

Suppose that the maximum membership on one year’s record is located at then the year’s record is viewed as _A.

6. Construct the fuzzy forecasting model.

Let R(1) be the first fuzzy relational ^matrix, which can be written as

358 ^Iflgfl

^{R(1)=F(1)T X} F(2) (16)

The elements of ^R(l) is defined as

r=rnin(F(l), F(2)1) ⁽¹⁷⁾

^Where Y(lf represents ^{for the i-th element of Y(1), and for the j-th} elements of Y(2). For all the historical knowledge, the fLizzy relational functions are found and union operator is applied to obtained the model:

R=Union of R(i) ⁽¹⁸⁾

7. Obtained forecasted output data using R.

As the model equation is ^determined, historical data can be used to obtained the predicted values by

F(t)=F(t-1) R ⁽¹⁹⁾

8. Transfer the output fuzzy set into forecasted records.

Since the output fuzzy ^results, they should be transfer into real numbers. The three-principle method ^[5] for the transformation is used in this study.

From the above ^{calculations,} the results of Song and Chissom method ^(the first- order ^model) are obtained. For comparison, a high-order fuzzy time series model is developed for the same forecasting enrollments. All the output fuzzy sets for the first-order model are ^useful, and they only serve as one of the possibility _F7

of the final output fuzzy sets of the high-order model. Following the same

processes, for example, the second possibility of the final output fuzzy sets _F12 are calculated as follows ^(Note that step 1-4 are the same as the first-order

model) Then

^(5*) Setup the two-step-ahead fuzzy relations based on historical knowledge.

When all the historical data are transferred into linguistic expressions, the logical relations can be constructed. Note that a two-step-ahead projection is applied instead of one-step-ahead projection used in step 5 of the first-order model.

(6*) Construct the two-step-ahead fuzzy forecasting model _R22.

Let R(1) be the first fuzzy relational function, which can be written as

_R22 ^{(1)=F(1)T X} F(3)

_R22 (2)=F(2)T ^X F(4) (20)

359

For example, the elements _ru of _R22 ⁽¹⁾ is defined as

r,1=min(F(1),, F(3)1) ⁽²¹⁾