В дифференциальном уравнении в явном виде отсутствует независимая переменная

Пример 9

Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям  ,  , 

Решение: В данном уравнении в явном виде не участвует переменная  . Подстановка здесь более замысловата. Первую производную   заменим некоторой пока еще неизвестной функцией  , которая зависит от функции «игрек»:  . Обратите внимание, что функция   – это сложная функция. Внешняя функция – «зет», внутренняя функция – «игрек» («игрек» сам по себе является функцией).

Находим вторую производную. По правилу дифференцирования сложной функции:

Учитывая, что  , окончательно получаем: 

В принципе, можно запомнить данную замену формально и коротко:

Другой вопрос, что студентам часто не понятно, почему в замене такая странная вторая производная:  , «совершенно же очевидно, что должно быть  ». А вот, оно, и не очевидно. Почему  , я только что подробно прокомментировал.

Итак, в исходном уравнении   проведём нашу замену:

Цель замены – опять же понизить порядок уравнения:

Одно «зет» сразу сокращаем:

Получено уравнение с разделяющимися переменными. Если   – функция, зависящая от «игрек», то первая производная в дифференциалах расписывается так: . Не допускаем машинальной ошибки – не пишем «привычное»  !!!

Разделяем переменные и интегрируем:

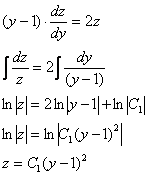
Проведем обратную замену  :

Как и в первом параграфе, константу целесообразно отстрелить незамедлительно, это значительно упростит дальнейшее интегрирование.

Используем оба начальных условия одновременно:  , 

В полученное уравнение   подставим   и  :

Таким образом:

Дальнейшее просто:

Вторую константу тоже отстреливаем. Используя начальное условие  , проводим подстановку  :

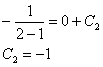
Таким образом: 

Выразим частное решение в явном виде:

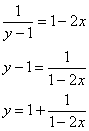
Ответ: частное решение: 

Пример 10

Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям  ,  , 

Решение: В данном уравнении в явном виде не участвует переменная  . Еще здесь нет первой производной, но это не должно смущать – важно, что нет «иксов», а значит, используется стандартная замена:

Таким образом, степень уравнения понижена до первого порядка:

Разделяем переменные и интегрируем, не забывая, что  :

Переобозначим константу   через  : .

Проведём обратную замену  :

Используем одновременно оба начальных условия  ,   и найдём значение константы  . Для этого в полученное уравнение   подставим   и :

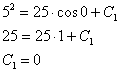
Таким образом:

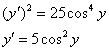
Разделяем переменные и интегрируем:

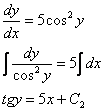
В соответствии с начальным условием  : 

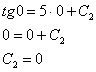
Окончательно:   или 

Ответ: частное решение: 

Пример 11

Найти решение задачи Коши. ,  , 

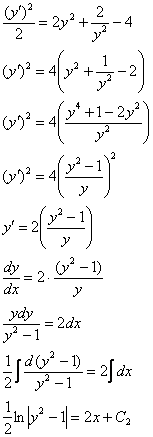Решение: В данном уравнении в явном виде не участвует переменная  , проведем замену:  Обратная замена:  В соответствии с начальными условиями  ,  : В соответствии с начальным условием  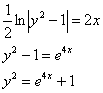:  Ответ: частное решение: 

Пример 1

Решить дифференциальное уравнение 

Решение: составим и решим характеристическое уравнение:

,  Получены два различных действительных корня (от греха подальше лучше сразу же  выполнить проверку, подставив корни в уравнение).  Всё, что осталось сделать – записать ответ, руководствуясь формулой 

Ответ: общее решение: 

Пример 3

Решить дифференциальное уравнение 

Решение: составим и решим характеристическое уравнение: Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения: (конечно, формулу нужно увидеть, это приходит с опытом решения)

Получены два кратных действительных корня 

Ответ: общее решение: 

Пример 7

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  , 

Решение: составим и решим характеристическое уравнение: ,  Получены два различных действительных корня, поэтому общее решение:

Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Наша задача состоит в том, чтобы найти ТАКИЕ значения констант  , чтобы выполнялись ОБА условия. Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие  : Согласно начальному условию, получаем первое уравнение:   или просто 

Далее берём наше общее решение   и находим производную: Используем второе начальное условие  : Согласно второму начальному условию, получаем второе уравнение:   или просто 

Составим и решим систему из двух найденных уравнений:

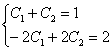
Допустимо использовать «школьный» метод решения, но в высшей математике чаще применяют метод почленного сложения/вычитания уравнений системы, посетите соответствующий урок, если не знакомы с методом.

В составленной системе удобно разделить второе уравнение на 2 и почленно сложить уравнения:

Всё, что осталось сделать – подставить найденные значения констант   в общее решение  :

Ответ: частное решение: 

Пример 2: Решение: Составим и решим характеристическое уравнение: ,   – различные действительные корни Ответ: общее решение:  Проверка: Найдем производную: Найдем вторую производную: Подставим   и   в левую часть исходного уравнения  : , таким образом, общее решение найдено правильно.

Пример 4:  Решение: составим и решим характеристическое уравнение: Получены два кратных действительных корня  Ответ: общее решение: 

Пример 6:  Решение: Составим и решим характеристическое уравнение:  – сопряженные комплексные корни Ответ: общее решение: 

Пример 8: 

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям  ,  . Выполнить проверку.

Решение: Составим и решим характеристическое уравнение:  – получены сопряженные комплексные корни, поэтому общее решение: Найдем частное решение, удовлетворяющее заданным начальным условиям: , то есть  , (значение константы получилось сразу же). .  То есть  . Составим и решим систему: 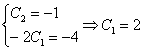Ответ: частное решение:  Проверка:   – начальное условие выполнено.  – второе начальное условие выполнено. Подставим   и   в левую часть исходного уравнения: Получена правая часть исходного уравнения (ноль). Такие образом, здание выполнено верно.

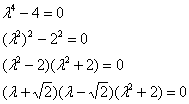
Пример 10: Решение: Составим и решим характеристическое уравнение: ,   – получены два различных действительных корня и два сопряженных комплексных корня. Ответ: общее решение 

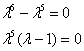
Пример 11:  Решение: Составим и решим характеристическое уравнение: ,   – получены пять кратных  нулевых корней  и действительный корень  Ответ: общее решение

Пример 1. Дано следующее дифференциальное уравнение второго порядка: y'' + y'/x + y = 0. Необходимо привести его к системе уравнений первого порядка.

Обозначим: dy/dt = z; d²y/dt² = z'. Тогда: z' + z/x + y = 0. И далее приходим к системе дифференциальных уравнений первого порядка:

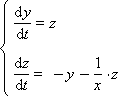
Далее решаем эту систему уже известными нам способами, например, методом Эйлера