7.4.2. Метод пятизначной логики

Этот метод является одной из разновидностей ДСМ-метода и применяет для оценки истинности высказываний расширенную границу шкалирования.

Традиционно в ДСМ–логике используется четыре типа истинностных значений для оценки: +1 – истина, -1 – ложь, 0 – противоречие,  – неопределенность.

Однако часто такой шкалы недостаточно – так ответ «не знаю, затрудняюсь ответить» можно рассматривать по-разному. Если есть аргументы «за» и аргументы «против»– тогда это 0 – противоречие, если же информация у опрашиваемого отсутствует, то тогда необходимо ввести дополнительное состояние  – отсутствие информации. Таким образом, используемая логика типов истинностных значений оказывается пятизначной. Такое расширение границ шкалирования позволяет более точно работать с методом.

7.4.3. Алгоритм древ

Данный алгоритм является методом качественного обобщения по признакам и предложен как развитие алгоритма обобщения Э. Ханта – CLS.

В основе метода используется дерево решений – один из способов разбиения множества данных на классы или категории. Решающее дерево классифицирует примеры в конечное множество классов. Вершины дерева, не являющиеся концевыми, помечены именами атрибутов, ребра – допустимые значения этого атрибута, концевые вершины – имена классов. Процесс классификации заключается в прохождении пути по дереву по ребрам, соответствующим значениям атрибутов объекта.

Идея алгоритма состоит в следующем: ставится задача построения обобщенного понятия на основе анализа обучающей выборки S, содержащей примеры К⁺ и контрпримеры К^-. При этом формируется логическая функция принадлежности к обобщенному понятию, которая служит классифицирующим правилом. В этой логической функции переменные, отражающие значения признаков, соединены операциями конъюнкции, дизъюнкции и отрицания.

На первом этапе работы алгоритма делается попытка сформировать обобщенное конъюнктивное понятие на основе поиска признаков, значения которых являются общими для всех объектов выборки К⁺ и не встречаются среди контрпримеров К^-. Результатом должна стать логическая функция П_к, значение которой равно 1 на всех примерах из К⁺ и равно 0 на всех контрпримерах из К^-.

Затем формируется обобщенное дизъюнктивное понятие П_д, построение которого начинается c выбора среди элементов К⁺ такого признака А_i , который является наиболее существенным для обобщенного понятия. Для выбранного признака ищется значение F, которое называется разделяющим значением, так как на его основе происходит разбиение выборок К⁺ и К^- на две пары подвыборок: К⁺¹ и К^-1, К^+-1 и К^--1.

7.4.4. Алгоритм амх (алгоритм, основанный на метрике Хемминга)

Дерево решений – это алгоритм, представленный в специальной форме. Алгоритм АМХ – это алгоритм, который строит бинарное дерево решений на основе поиска существенного (разделяющего) признака. Каждой вершине приписывается вопрос «Обладает ли пример данным значением признака?», а дуги взвешиваются ответами «Да» и «Нет». Конечные вершины дерева будут помечены утверждениями, соответствующим решениям.

Распознавание начинается с корневой вершины, откуда строится путь до конечной вершины. В каждом внутреннем узле необходимо отвечать на вопрос и выбирать соответствующую дугу, ведущую к следующему вопросу. Вершины с одинаковыми вопросами могут несколько раз встречаться в дереве, но в каждом конкретном пути от корня к листу каждый вопрос встретится всего один раз.

Рассмотрим рекурсивный алгоритм построения бинарного дерева на основе обучающей выборки S.

Для предъявляемой обучающей выборки S ищется наиболее важный вопрос, который помещается в корневую вершину дерева. Обучающее множество S в соответствии с ответами («Да, «Нет») делится на две подвыборки. Далее для каждой подвыборки снова ищется наиболее важный вопрос, и порождаются по две новые ветви. Процесс завершается, когда использованы все вопросы.

Для нахождения наиболее важного вопроса используется следующий подход. Предположим, что обучающее множество S содержит К примеров. Построим метрику на множестве вопросов и упорядочим S по следующему правилу.

Для каждого вопроса Q строится К-арный кортеж, где j-е значение в кортеже имеет значение:

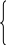
1, если j-й пример из S дает ответ «Да» на вопрос Q,

j =

0 – в противном случае.

Расстояние между двумя вопросами определяется как расстояние между двумя двоичными векторами по Хеммингу. Обозначим такое расстояние между векторами X и Y как H_d(X,Y). При этом из рассмотрения исключаются вопросы, на которые все примеры из S дают одинаковый ответ. Для искомого свойства Р строится К-арный кортеж на всех объектах S по правилу: j-е значение в кортеже Р равно 1, если j-й пример из S обладает искомым свойством Р, и 0 – если не обладает. Чтобы выбрать наиболее важный вопрос, необходимо найти среди всех подходящих вопросов Q такой, чья связь со свойством Р наиболее тесная. Для этого используется следующее правило: p_m=min(H_d(P,Q), K–H_d(P,Q)), т.е. берется наименьшее расстояние по Хеммингу от Q до P и от Q до –P.

Когда наиболее важный вопрос выбран, выполняется расщепление обучающего множества на S_да и S_нет, затем для каждого из них выполняются аналогичные вычисления.