6.1.1. Операции над предикатами

1. Пусть заданы два предиката P(x), Q(x) (x M). Конъюнкцией этих предикатов называется предикат, который принимает значение «истина» только для тех значений x, для которых каждый из предикатов P и Q принимает значение «истина»:

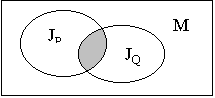J_PQ = J_P  J_Q

2. Пусть заданы два предиката P(x), Q(x) (x M). Дизъюнкцией этих предикатов называется предикат, который принимает значение «ложь» только для тех значений x, для которых каждый из предикатов P и Q принимают значение «ложь»:

J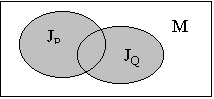 _PQ = J_P  J_Q

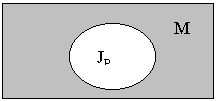
3. Пусть заданы два предиката P(x), Q(x) (x M). Отрицанием одноместного предиката называется предикат ¬Р(x), который принимает значение «истина» для всех значений x, для которых Р(x) ложно:

J_¬P = M - J_P

4. Пусть заданы два предиката P(x), Q(x) (x M). Импликацией Р(x) в Q(x) называется предикат, для всех x которого Р(x) истинно, а Q(x) ложно:

J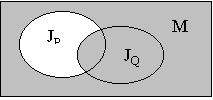 _PQ = J_P \ (J_Р & J_Q)

5. Пусть заданы два предиката P(x), Q(x) (x M). Эквивалентностью Р(x) и Q(x) называется предикат, для всех x которого истинна конъюнкция предикатов Р(х) и Q(x) или истинна конъюнкция предикатов ¬Р(х) и ¬Q(x):

J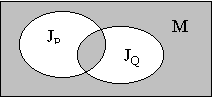 _PQ = (J_Р & J_Q)  ( J_¬Р & J_¬Q)

6.1.2. Общезначимость и выполнимость формул исчисления предикатов

Понятия общезначимости и противоречивости формул, введенные в исчислении высказываний, сохраняют свою силу и для исчисления предикатов.

Формула исчисления предикатов называется выполнимой в области М, если существуют значения xМ, при которых формула принимает значение «истина».

Формула исчисления предикатов называется выполнимой, если существует область, на которой она выполнима.

Формула исчисления предикатов называется тождественно истинной в области М, если она принимает истинные значения для всех значений входящих в нее переменных, отнесенных к области М.

Формула исчисления предикатов называется общезначимой, если она тождественно истинна на любой области.

Формула тождественно ложна в области М, если она принимает значение «ложь» для всех значений входящих в нее переменных, отнесенных к области М.

Формула невыполнима, если она тождественно ложна на всякой области.

Из вышесказанного следует, что существует два основных класса формул исчисления предикатов – выполнимые и невыполнимые.

6.2 Исчисление предикатов как формальная система

Рассмотрим формальную аксиоматическую систему для исчисления предикатов.

1. Алфавит:

а) счетное множество предметных переменных x₁, x₂, …, x_n …;

б) конечное (может быть и пустое) или счетное множество предметных констант а₁, а₂, …;

в) конечное (может быть и пустое) или счетное множество функциональных букв f_1, f₂, …, f_k, …;

г) конечное (может быть и пустое) или счетное множество предикатных букв А₁, А₂, …;

д) символы логических операций , , , , ;

е) символы кванторов , ;

ж) скобки ( ) и запятая.

2. Правила построения синтаксически правильных формул:

а) всякий атом есть формула;

б) если А и В – формулы и х – предметная переменная, то каждое из выражений А, А В, АВ, АВ, АВ, хА, хА есть формула.

3. Система аксиом. Систему аксиом исчисления предикатов составляют система аксиом исчисления высказываний и две дополнительные аксиомы:

а) х А(х)А(t), где А(х) – есть синтаксически правильная формула и t – терм, свободный для х в А(х);

б) А(t) х А(х), где А(х) – есть синтаксически правильная формула и t – терм, свободный для х в А(х).

4. Правила вывода:

а) все аксиомы выводимы;

б) правило подстановки термов t₁, t₂, …, t_n вместо х_i1, х_i2,… х_ir в А[х_i1, х_i2,… х_ir] такой, что А[х_i1, х_i2,… х_ir] свободна для t₁, t₂, …, t_n;

в) правило modus ponens;

г) правило обобщения (или правило связывания квантором всеобщности) – если синтаксически правильная формула В А(х) при условии, что В не содержит свободных вхождений х, выводима, то выводима будет и формула В х А(х);

д) правило конкретизации (или правило связывания квантором существования) – если А(х)  В есть выводимая синтаксически правильная формула (теорема) и В не содержит свободных вхождений х, то х А(х) В также теорема;

е) если А – теорема, имеющая квантор всеобщности и/или квантор существования, то одна связанная переменная в А может быть заменена другой связанной переменной, отличной от всех свободных переменных, одновременно на всех областях действия квантора и в самом кванторе.

Для исчисления предикатов также справедливы следующие теоремы, касающиеся его непротиворечивости и полноты:

1. Исчисление предикатов первого порядка непротиворечиво.

2. Во всяком исчислении предикатов первого порядка всякая теорема является общезначимой формулой.

3. Во всяком исчислении предикатов первого порядка всякая общезначимая формула является теоремой (теорема Геделя о полноте).

Исчисление предикатов – пример неразрешимой формальной системы. Неразрешимость исчисления предикатов доказал в 1936 г. американский логик Алонзо Черч. В доказанной им теореме говорится об отсутствии эффективной процедуры при решении вопроса относительно произвольной формулы формальной системы, содержащей арифметику натуральных чисел, является ли эта формула теоремой.

6.3. Пренексные нормальные формы исчисления предикатов

В исчислении высказываний были рассмотрены две нормальные формы высказываний – КНФ и ДНФ. В исчислении предикатов также имеется нормальная форма, так называемая пренексная нормальная форма (ПНФ).

Говорят, что формула F исчисления предикатов находится в ПНФ тогда и только тогда, когда ее можно представить в форме ₁х₁₂х₂ … _rх_r М, где каждый _iх_i, i =1, 2, …, r есть либо x_i, либо x_i и М – бескванторная формула. Иногда ₁х₁₂х₂ … _rх_r называют префиксом, а М – матрицей формулы F.

Например, формула F₁= xy(Q(x,y)P(f(x))R(x,g(y))) находится в ПНФ, а формула F₂ = x(P(x)  yQ(x,y)) – не в ПНФ.

Существует простой алгоритм, преобразующий произвольную заданную формулу в равносильную ей формулу, имеющую пренексный вид. Алгоритм состоит из следующих шагов.

1. Исключение логических связок эквивалентности и импликации. Многократно (пока это возможно) применяется следующее правило: найти самое левое вхождение связок  или  и сделать замены: FФ = (FФ)(FФ); FФ = FФ.

2. Продвижение знака отрицания до атома. Многократно (пока это возможно) делаются замены:  F = F;

(FФ) = FФ;

(FФ) = FФ;

xF(x) = x( F(x));

x F(x) = x(F(x)).

3. Переименование связанных переменных. Переименовать связанные переменные таким образом, чтобы ни одна из переменных не имела одновременно и свободных и связанных вхождений. Многократно (пока это возможно) применяется следующее правило: найти самое левое вхождение переменной такое, что это вхождение связано (некоторым квантором), но существует еще одно вхождение этой же переменной; затем сделать замену связанного вхождения на вхождение новой переменной.

4. Удаление квантификаций, область действия которых не содержит вхождений квантифицируемых переменных.

5. Вынесение кванторов. Используются следующие равносильности:

1. xF(x)Ф = x(F(x)Ф);

2. xF(x)Ф = x(F(x)Ф);

3. xF(x)xФ(x) = x(F(x)Ф(x));

4. xF(x) xФ(x) = x(F(x)Ф(x));

5. ₁xF(x) ₂xФ(x) =₁x ₂y(F(x)Ф(y));

6. xF(x)  ₂xФ(x) =₁x ₂y(F(x) Ф(y));

где , ₁, ₂ – кванторы либо , либо .

После выполнения пятого шага формула приобретает пренексный вид.