5.4. Понятие семантического дерева

Если Р={Р₁…Р_n} – множество высказываний, то семантическое дерево – это бинарное дерево, удовлетворяющее следующим условиям:

1. каждая дуга помечена негативной или позитивной литерой из множества Р;

2. литеры, которыми помечены две дуги, выходящие из одного узла, должны быть противоположны;

3. никакая ветвь (путь) на дереве не содержит более одного вхождения каждой литеры;

4. никакая ветвь не содержит пары противоположных литер.

Например, для множества литер P={p, q} семантическое дерево имеет вид:

А для множества литер P={p, q, r} семантическое дерево имеет вид:

Каждому узлу N семантического дерева соответствует функция I_n, которая сопоставляет истинностное значение некоторым элементам из множества Р и называется частичной интерпретацией. Частичная интерпретация I_n сопоставляет значение Т или F высказыванию р, если некоторая дуга из корня N помечена р или (┐p). Частичная интерпретация не определена для высказывания р, если р и (┐p) не встречается на пути из корня в N.

Семантическое дерево полное, если каждый его лист соответствует некоторой всюду определенной интерпретации. Для того чтобы определить, выполнима ли формула А, с помощью алгоритма полного перебора требуется просмотреть полное семантическое дерево, соответствующее высказываниям, встречающимся в формуле А. Формула выполнима, если хотя бы для одного листа А получается значение Т. Этот алгоритм не эффективен, т. к. требуется просматривать 2ⁿ интерпретаций.

5.5. Алгоритм Куайна

Алгоритм Куайна, или алгоритм частичного перебора, позволяет доказать общезначимость формулы без просмотра полного семантического дерева. Основная идея алгоритма заключается в следующем: если при всех возможных расширениях некоторой частичной интерпретации формула А принимает одно и то же истинностное значение, то бесполезно строить поддерево, исходящее из узла, соответствующего этой частичной интерпретации. Рассмотрим работу алгоритма на примере.

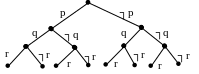
Пример. Проверить общезначимость формулы (((pq)r) (pq))(pr).

1. Упорядочим множества элементов высказываний: {p, q, r}. Это эквивалентно тому, что дуги уровня 1 помечены литерой р, уровня 2 – литерой q, а уровня 3 – литерой r.

2. Рассмотрим те интерпретации, при которых р есть Т. При этом исходная формула сводится к формуле ((qr) q) r.

3. Далее q интерпретируем как Т, тогда формула принимает вид r r – общезначимая формула.

4. Далее q интерпретируем как F, тогда формула принимает вид Fr – тоже общезначимая формула, поэтому дальше строить поддерево не нужно.

5. Далее, рассмотрим те интерпретации, при которых p принимает значение F, тогда исходная формула имеет вид (Fr) T) T – общезначимая формула. Следовательно, исходная формула всегда принимает значение Т, т.е. является общезначимой.

Этому примеру соответствует построение части семантического дерева, показанной на рисунке.