10.Хантуш математикалық моделін қорыту және механикалық мағанасы.

2блок

9) Ракетаның ұшу траекториясын бірінші ретті дифференциалдық теңдеулер жүйесімен берілген Коши есебімен модельдеу.

dθ/dt=-g/(ϑ(t)) cos⁡〖θ 〗 (13)

dx/dt=ϑ cos⁡〖θ(t)〗 (14)

dy/dt=ϑ sin⁡〖θ(t)〗 (15)

dm/dt=-f(t) (16)

x(0)=0,y(0)=0,x ̇(0)=0,y ̇(0)=0,θ(0)=θ_0,m(0)=M (17)

x(0)=0,y(0)=0,ϑ(0)=0,θ(0)=θ_0,m(0)=M (18)

Қорытынды:

Т=0,m=15

dϑ/dt=-(cSρϑ^2)/2m-g sin⁡θ (19)

Бұрышқа байланысты теңдеуі:

dθ/dt=-g/(ϑ(t)) cos⁡〖θ ̇ 〗 (20)

dx/dt=ϑ cos⁡θ (21)

dy/dt=ϑ sin⁡θ (22)

x(0)=0,y(0)=0,ϑ(0)=ϑ_0,θ(0)=θ_0 (23)

8Механикалық және электірлік тербелістерді сипаттайтын парметрлер арасындағы аналогия (ұқсастық).Электрлік тербелісті моделдеу үшін заряд,ток,кернеу,сыйымдылық,индуктивтік т.б. электрлік шама-ң анықтамасын білу керек.Мысалы ток дегеніміз-өткізгіштегі заряд-ң меншіктелген қозғалысы,бағыты оң заряд-ң бағытымен анықталады.

Ан-ма:Бірлік уақытта бірлік қимадан өтетін заряд-ң өзгеріс-ң шамасы.

ток,кернеу

конденсатор сиымдылығы

u=

Электр тізбек

(3)

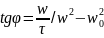
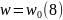
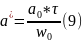
Э.қ.к=0

Э.қ.к 0

3блок

11.Толық электрлік тізбектің математикалық моделі

Электр тізбегі

Q-заряд, J= -ток, U- кернеу, L-индукция, -релаксация уақыты , =

Т олық электрлік тізбек алайық

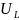J = , =JR , = Q , =L

Толық электрлік тізбек, тізбектей жалғанған

ЭҚК С

L =

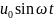
L Q+RJ=

L =

+ Q=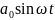 (1)-заряд б/ша жазылған еріксіз тербеліс

= , = ,

Q(t)=a (2)-жалпы шешім б/ды

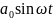
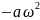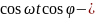
+ a +a =

[ + ]+ ( )+a ( +

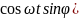
= ,енді топтастырайық

]+ ]

(4)-шарт қоямыз

=0

a= (5)

,

tg , (6)-фазалық ығысу

a= (7) , б/са резонанс құбылысы байқалады

a*=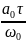 (9) , релаксациялық уақыт

12)Электірлік тербелістің периодты және жиілігінің формуласы. Электрлік тербелісті моделдеу.

Электрлік тербелісті моделдеу үшін заряд,ток,кернеу,сыйымдылық,индуктивтік т.б. электрлік шама-ң анықтамасын білу керек.Мысалы ток дегеніміз-өткізгіштегі заряд-ң меншіктелген қозғалысы,бағыты оң заряд-ң бағытымен анықталады.

Ан-ма:Бірлік уақытта бірлік қимадан өтетін заряд-ң өзгеріс-ң шамасы.

ток,кернеу

конденсатор сиымдылығы

u=

Электр тізбек

(3)

Э.қ.к=0

Э.қ.к 0

13)Тұтқырлық үйкеліс күштің әсеріне байланысты тербелісті модельдеу.

Субстанциялық туындысы бойынша берілген қозғалыс теңдеуі.

Қозғалыс теңдеуінің векторлық жазбасы.

1. (2 (3) (4) (5)

(1)

=0 (2)

1 – Бірлік көлемдегі қозғалыс мөлшерініңайналу жылдамдығы.

2 – Бірлік көлемдегі конвенциялық тасымалдану әсерінен қозғалыс мөлшерінің жиналу жылдамдығы.

3 – Бірлік көлемге шағылған қысым күші.

4 - Бірлік көлемдегі тұтқырлық күштің (яғни жылдамдықтар градиенті) тасымалдану әсеріне байланысты қозғалыс мөлшерінің тасымалдану жылдамдығы.

1. - ші теңдеудегі (2) және (4), яғни [ ] және [ ] тензорлық табиғатына байланысты дивергенциялық амалдарды қарастыруға болмайды.

Қозғалыс мөлшерінің х компоненттеріне тәуелді қосындысына келесі амалды қолданайық.

Бірлік көлемдегі массаның сақталу балансы: (3)

1. – ші теңдеуді қозғалыс мөлшерінің х компоненті бойынша алайық.

,

(2)-ші теңдікті ескеріп:

Немесе

х - құраушысы бойынша субстанциялық туынды.

Субстанциялық туындысы қалған у және z - құраушылары бойынша:

Жалпы векторлық жазбасы:

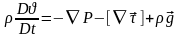(4)

1. (2) (3) (4)

1 – Бірлік көлемнің массасына көбейтілген үдеу.

2 – Бірлік көлемге шағылған қысым күші.

3 – Бірлік көлемге шағылған тұтқырлық үйкеліс күш.

4 – Бірлік көлемге шағылған ауырлық күш.

2. –ші теңдеуді Ньютонның 2-ші заңын ескеріп тұжырымдасақ сұйықпен бірге қозғалған бірлік көлемдік элементке әсер еткен күштердің нәтижесінде алған үдеумен қозғалысы масса*үдеу=күштер қысымы.