8.Көптүйіліскен аймақ үшін сығылмайтын сұйықтың фильтірлену есебінің математикалық моделі.
9.Мятиев -Гиринский математикалық моделін қорыту және механикалық мағанасы.
Өтімділігі
нашар
қатпарымен төбесінен жабылған , өтімділігі
жақсы К , ал қуаты Н , ұзындығы L пластағы
флюидтің фильтрациялық тасмалдануының
математикалық моделін қоялық.
Қ
ос
пластық жүйенің x=0 қимасынан өндірілетін
флюид мөлшері Q, ал етегі бойынша қоршаған
ортамен флюид алмасу болмайды, ал жүйенің
бастапқы
=150
ат қысымдағы жағдайы тұрақты.
y
b
x
H K
L
Ω = {0<x<L, 0<y<-H};
b << KH;
b << H.
Математикалық модель келесі заңдар
Әлсіз сығылатын флюидтің үзіліссіздік заңын келесі түрде:
+
div
= 0,
Дарси заңы:
=
-
gradP,
Флюид күйін сипаттайтын теңдеу:
=
(1+
(P-
)),
Кеуек орта:
=
+
(P-
),
Мұнда 3 және 4 теңдеулерді 1 қысым, сұйық массасының
+
div
= 0
(*)
үзіліссіздік теңдеуін басқаша жазамыз
=
+
- сиымдылық серпімдісі
=
(
)
+
(
)
, (x,y)
Ω = {0<x<L, -H<y<0} (1)
P(x,y,0) = , (x,y) (2)
dy=Q,
x=0,
=0,
t
0
(
)
P(0,
-H
)
=
,
t
0
(
)
,
=0
(
)
P(x=L,
-H
)
=
,
t
0
(
)
=
(
)
,
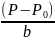P
=P
,
t
0
(5)
P(0
0)
= 0
(6)
Орташаланған қысым енгіземіз.
P(x,t)
=
(7)
=
dy;
=
6-шы 5-ші жартысы
(P-
)
,
0
0
(1)
P(x,0)=
,
0
(2)
P(0,t)
= Q,
0
(
)
P(0,t) = , t 0 ( )
0
(
)
,
t
0
(
)
+
ᵞ(
),
x
t
0
(1)
-
пьезоөткізгіштік
коэф.
ᵞ
=
- гидро
коэф.
(1), (2), ( ) және ( ) бірінші ретті және айырымдық, осымен бірге интегралдық шешімін
ᵞ
=
-
,
,
,
,
;
P
=
= 30;
=
-
,
+
,
x
t
0
(1)
P(x,0)=1,
0
(2)
P(0,t)=1, t 0 (3)
P(1,t)= , t 0 (4)
Интегралдық шешімі (1) - (4)
,
(
)
(
)
(t)=
ᵞ
(
)
=
(
)
(
)
=
–
интегралдық
теңдеу жұмыс кіретін шекаралық шарттар
бойынша есептеледі
– жүйедегі
сай
флюид өзгерісін береді– жүйедегі бастапқы t=0 моменті уақытына сай флюид моменті
– жүйенің x=1 қимасынан енетін флюид мөлшері
- жүйенің x=0 қимасынан тасмалданатын флюид мөлшері
– жүйенің ᵞ-коэф. Байланысты төбесінен тасымалданатын қоюдың мөлшері