6.Вольтерр-Лотка теңдеуінің фазалық жазықтықтағы сипаттамасы.

7.“Жыртқыш-Жемтік” математикалық моделінің кинематикалық сипаттамасы.

(1),

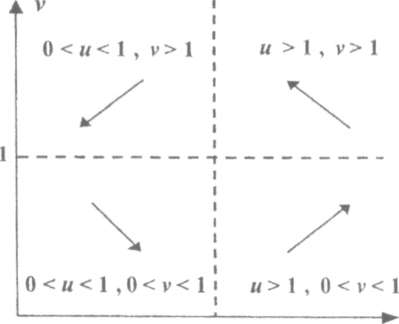
Зерттелінетін (1) тендеу бойынша фазалық жазықтықта төрт аймақ бар, осы аймақтардағы жүйенің қасиеттеріне байланысты сипаттамалары әртүрлі (1-сур. қара). Егерде кейбір t уақыт моментінде мынадай теңсіздік орнасын 0 < u(t) < 1 , 0 < v(t) < 1 , (2) бірінші (2) тендеудің оң жағы оң, ал екінші теріс. Онда мынадай теңсіздік орындалады , ендеше u - функция уақытқа байланысты өседі, ал v кемиді (2 сур. қара).

1 и

1 Сурет. "Жыртқыш-жемтік" моделінде жүйе эволюциясының бағыты.

(2) формула орындалғанша барлық уақытта жүйенің сипаттамасы өзгермейді. Егерде өсу процесі кезінде функция u - мәні бірден асып кетсе, немесе функия v - азайып нөлге жетсе, бұл шарт бұзылады. Екінші (1) тендеу бойынша v - мөні нөлге жуықтағанда, осымен бірге оның туындысы да нөлге ұмтылады. Сондықтан, функция v - нөлге жақындауы асимптотикалық түрде жүреді. Бірақ функция u - өсуімен және v - кемуімен u - туындысы оң әрі өседі. Осыдан ерте ме, кеш пе u - мәні бірден асады, сөйтіп мынадай теңсіздік орындалады

u(t) > 1 , 0 < v(t) < 1 . (3)

Мұндай шарттар үшін екі функцияның туындысы да оң, ендеше мәндері уақытқа байланысты өседі. Бұл сипаттама (3) теңсіздік орындалғанша, барлық уақытта өзгермейді. Түбінде функция v өсіп бірден асады, нәтижесінде мынадай теңсіздік орындалады u(t) > 1 , v(t) > 1 , (4). Осы сәттен бастап функция и кемиді, ал v шамасы осы уақыттан бастап өседі. Сөйтіп (4) қатынастың біреуі өзгергенде жағдай өзгереді. Түбінде и функция уақытқа байланысты біртіндеп кеміп, бірден кіші болады жөне мынадай теңсіздік жазамыз: (5)

Бұл, қарастырылатын екі функцияның кемитінін көрсетеді. Функция u біртіндеп нөлге жақындағанда, оның туындысы да нөлге ұмтылғанын ескерсек, онда и - оң мәнінде, бір уақыт моменті туып v - шамасы бірден кіші болады. Тағы да (2) катынас орындалады, ендеше сипаттаған процесіміз қайталанады.

Теңдеу (1) шешімі периодты функция екенін көруге болады (2-сур.қара). Ал фазалық жазықтағы қисық тұйық болады. Фазалық жазықтагы v координат өсінде жатқан жүйе күйі, тривиалдық қалпына ұмтылады деуге болады. Басқа фазалық қисықтар кейбір уақыт ішінде координат басына жақындауы мүмкін, бірақ артынан сөзсіз алшақтайды (1-сур.қара). Сөйтіп, ершік деп аталатын орнықсыз тепе- тендік қалпын аламыз. Бастапқы момент уақытында жемтік пен жыртқыштың сан мөлшері аз болсын деп жориық. Жемтіктің бастапқы сан мөлшері аз болғандықтан жыртқыштын саны азаяды, сөйтіп жемтікгің табиғи жауы аз болғандықтан жемтіктің түлеп-өсуі артады. Басы аз жыртқыштар үшін саны өскен жемтіктер жақсы қорек болады ,сөйтіп екінші этапта жыртқыштардың өсімі арта бастайды. Екінші этапта жемтіктің саны өскен сайын жыртқыштың түлеп-өсуі де тездейді. Үшінші этапта жемтіктің табиғи өсімі жыртқыштың оларды құртқан санымен теңдестірген уақытта басталады жөне осы уақыттан бастап жемтіктердің өсімі азая бастайды. Ары қарай жыртқыштардың популяциясы өседі, ал жемтіктердің өлім- жітімі көбейеді. Бұл этапта жемтіктің өлім-жітімі көбейген сайын, жыртқыштың өсу санының жылдамдығы біртіндеп азаяды.

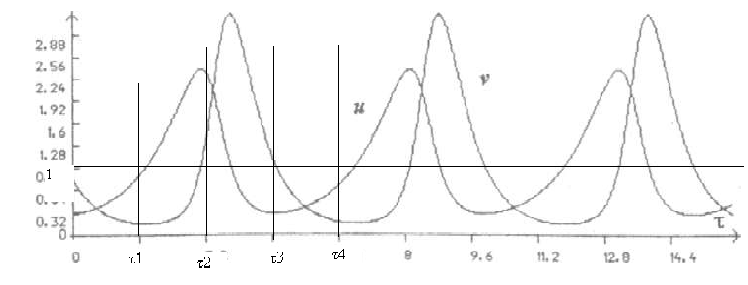
2-Сурет. "Жыртқыш-жемтік " моделінде күй функциясы периодты болады.

Түбінде бір уақыт моменті туып, өрбіп-өскен жыртқышқа қорек жетіспейді, енді жыртқыштардың саны азая бастайды. Жемтіктің жалпы санының азаю жылдамдығы кемиді, жыртқыштардың сан мөлшерінін төмендеуіне байланысты. Келесі уақыт моменті туып жсмтіктің өлім-жітімі өзінің минимум шамасына жетіп, енді жыртқыштардың санының кемуіне байланысты жемтіктің өрбіп - өсуі арта бастайды. Осыдан бастап жаңа цикл жүреді, сөйтіп бастапқы этап қайта басталады