40.Қозғалыс мөлшерін математикалық модельдеу және механикалық мағанасы.
Кеңістікте
ойша алынған көлем элементі үшін
сұйықтың стационарлық емес ағысының
қозғалыс мөлшерінің сақталу баланысының
теңдеуін қарастырайық. Әлсіз сығылатын
сұйықтың қарастырылатын
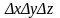элемент
үшін
алты қабырғасына байланысты ағынға
талдау жасап, қозғалыс мөлшерінің
баланысын жалпы түрде жазамыз [2]
(1-сурет):
Жалпы түрде (1)-ші жазылған қозғалыс мөлшерінің баланысы векторлық
теңдеу, сондықтан компоненттері бойынша және координаттар өстеріне жіктеп жазамыз.
(3.1)-ші баланстық теңдеудің х - компонентіне байланысты әр мүшесін талдап жазып, қалған у - және z компоненттері үшін де осылай талдаймыз. Қозғалыс мөлшерінің тасымалдануы екі механизммен жүреді: конвекциялық (сұйық көлемінің орын ауыстыруы) және молекулалық тасымалдануы (жылдамдық градиенті).
Сурет 2. - көлем элементіндегі сұйықтың қозғалыс мөлшерінің компоненттерінің өзгерісі стрелкамен көрсетілген.
Қозғалыс
мөлшерінің х
компонентінің көлем элементіне
байланысты (2-ші сурет) енген және шыққан
жылдамдығының өзгерісіне тиісті
баланысын қарастырайық. Конвекция
әсерінен координаты
болатын қыры бойынша
беттен
енген қозғалыс мөлшерінің х
-
компонентінің
жылдамдығы
,
ал осы көлем элементінің координаты
қырына тиісті беттен шыққан жылдамдығы
болады. Осы компонент векторының
координатасына тиісті қырына сәйкес
беттен
енген жылдамдығы
,
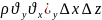ал
координатасына тиісті қырына сәйкес
беттен шыққан жылдамдығы
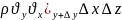болады. Өстіп,
координатасына тиісті қыры бойынша
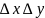беттен енген және шыққан қозғалыс
мөлшері
жане z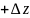
координатасы бойынша
беріледі.
Сонымен қозғалыс мөлшері векторының
компонентінің көлем элементінің алты
қимасына байланысты қосындысын келесі
түрде тұжырымдаймыз
.
Қозғалыс
мөлшерінің
компонентінің бақылаушы көлемге
байланысты молекулалық тасымалдануын
әр қыры бойынша осылай талдап жазамыз.
kоординатынан
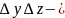беттен еніп,
координатынан
беттен молекулалық тасымалдануы
болады. Осы сияқты
kоординатынан
беттен еніп,
координатынан
беттен тасымалдануы
болса,
ал
және
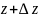kоординаттарынан
беттен тасымалдануын ескеріп, қозғалыс
мөлшерінің
компонентінің элементар бақылаушы
көлемге байланысты молекулалық
тасымалдануы
түрде жазылады.
Сөйтіп,
бұл қозғалыс мөлшерінің ағыны сұйықтың
тұтқырлық шамасының кернеулігіне
байланысты. Беттік ауданшаға
өсіне перпендикуляр түскен нормаль
және
- тангециал (жанама) кернеу
өсімен бағытталып,
координаттың қырына байланысты пайда
болады. Осыдан
өсіне тиісті күштер қосындысы қысым
айрымынан
және бірлік массаға шағылған ауырлық
күшінен
тұрады.
Қозғалыс
мөлшерінің
компонентінің элементтегі жиналу
жылдамдығы
тең болады. Осыдан қозғалыс мөлшерінің
жылдамдықтарын баланстық (3.1) теңдеуге
қойып және элемент мөлшеріне
бөліп, жеке мүшелерінің
,
және
өсімшелеріне байланысты нөлге ұмтылдырып
шекке көшсек, қозғалыс
теңдеуінің
компонентіне тиісті дифференциалдық
теңдеуін аламыз
.
(3.2а)