38.Үзіліссіздік теңдеудің механикалық мағанасы және моделін қорыту.

Үзіліссіздік теңдеуін қорыту үшін ойша кеңістікте бекітілген элементінен өтетін сұйық массасының сақталу баланысын жазайық (2-сурет):

Алдымен параллелепипедтің өсіне перпендикуляр екі тік қабырға беттен өтетін сұйық массасының баланысын алайық. Бірлік уақытта қырына байланысты енетін сұйық массасы болса, ал қырынан шығатын сұйық массасы болады. Өстіп қалған екі

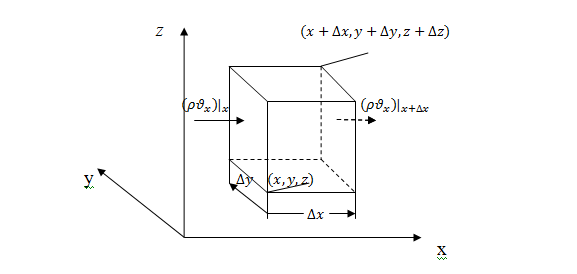
Сурет 1. Кеңістікте бекітілген көлемдік элементке байланысты сұйық ағыны.

қырына байланысты сұйық массасының тасымалдануын осыған ұқсас жазуға болады. Кеңістікте ойша алынған көлем элементіндегі сұйық массасының жиналу жылдамдығы тең. Сөйтіп, (2.1)-ші баланыстық теңдеуді келесі түрде тұжырымдауға болады

.

Бұл теңдеуді бөліп, көлем мөлшерін нөлге ұмтылдырып және шекке көшіп, үзіліссіздік теңдеуін аламыз

(2.2)

(2.2)-ші үзіліссіздік теңдеудің сипаттамасы, элементтегі массалық жылдамдық векторының өзгерісіне байланысты бекітілген нүктедегі сұйық тығыздығының өзгеру жылдамдығын береді. (2.2)-ші теңдеудің векторлық тұрпатын набла операторымен жазайық

. (2.3)

Мұндағы шама вектордың дивергенциясы делінеді де, немесе жазады. Сөйтіп, массалық ағын болса, ал дивергенцияның физикалық мағынасы бірлік көлемге шағылғандағы ағатын сұйық массасының жылдамдықтарының қосындысы. Сондықтан (2.3)-ші теңдеу бойынша кеңістікте бекітілген көлемнің өте аз ішкі элементіндегі тығыздықтың бірлік уақыт ішінде көбейуі осы элементке ағатын массасының жалпы жылдамдықтарын көлемге бөлгенге тең болады. Ал мұндағы Гамильтон операторы (“набла”) – градиент векторының орнына жазылатын символдық вектор, бірлік өлшемі , яғни ұзындық өлшеміне кері болады.

(2.2)-ші теңдеуді дифферециалдап және тығыздыққа байланысты туындыларды жинастырып, субстанциалық туындысын ескерсек, үзіліссіздік теңдеу келесі түрде жазылады

(2.4)

Үзіліссіздік теңдеудің (2.4) түрде жазылуы бақылаушының сұйық ағысымен бірге қозғала отырып, сұйық тығыздығының өзгеру жылдамдығын анықтау болады.

Бұл (2.3) теңдеу Эйлер жолы қолданылып алынған. Мұнда бақылаушы көлем бекітіліп, осы элементке байланысты ағатын сұйықтың балансы қарастырылады. Ал Лагранжаның балама жолымен алынған (2.4) теңдеуде бақылаушының элементпен бірге жылжып отырып сұйықтың қасиетін зерттеу жатады [1].

Табиғатта мүлде сығылмайтын сұйықтар болмайды, бірақ инженерлік тәжрибеде сұйықтың тығыздығын тұрақты жағдайда қарастыру есептің қойылымын жеңілдетеді және кейбір процесте жіберген қате шамасы аз болады, себебі сұйық қозғалысына сәйкес тоқ сызығындағы тығыздық тұрақты, ендеше

Егер сұйықтың тығыздығы тұрақты болса, онда сығылмайтын сұйықтың үзіліссіздік теңдеуін жазайық

, (2.5)

немесе декарт координаттар жүйесінде

Кеңістікте ойша алынған көлем элементі үшін сұйықтың стационарлық емес ағысының қозғалыс мөлшерінің сақталу баланысының теңдеуін қарастырайық.

3 9. Үзіліссіздік теңдеудің субстанциалдық тұрпатын модельдеу.

Кеңістікте ойша бекітілген элементті көлемдегі сұйық массасының байланысы үзіліссіздік теңдеуі делінеді. Осы элементтегі сұйықтың ағысының байланысы

Массаның Элементке Элементтен

Жиналу енетін массалық шығатын массалық

Жылдамдығы жылдамдығы жылдамдығы

V- кеңістіктегі векторлық өріс сы5ылатын (газ, сұйық) тегіс мех. орта - беттен шектелгенге дейін, ал газдың P – нүктесіндегі тығыздығы болсын . Осы t уақыт моментіндегі газдың массасы болса, онда уақыт бойынша өзгерісі dv

Сөйтіп V – көлемдегі, аз уақыт аралығында dv өзгереді,

яғни уақыт ішінде V көлемге сырттай енген газ(сұйық) мөлшері. Ал көлем ішінде газ пайда болмайды және жоғалып кетпейді.

Көлем ішіндегі сұйық массаның жиналуы ағыс беттен өтетін масса жылдамдығына байланысты.

- ds

-сыртқы нормальға жүргізілген массалық жылдамдықтың проекциясы -жоғары ретті аз шама болса, онда

dv = - ds

Ал, масса балансының сақталуын келесі түрде жазамыз

dv = - ds

Гаусс-Остраградский теоремасы бойынша беттен өткен массалық жылдамдықтың проекциясы, осы массалық ағынның дивергенциясы бойынша алынған көлемдік интегралды береді

=

осыдан

=0

Кез келген t уақыт моментінде көлемнің кез келген P нүктесінде орындалады

=0 (1)

(1)- масса ағынының үзіліссіздік теңдеуін -операторын алып жазайық

=0

=( субстанциялық туындысы бойынша жазайық

=0

(2)

Газ ( ) сығылмайтын қасиетін беретін масса ағынының үзіліссіздік заңы

(3)

Мұнда

=

Цилиндрлік коорд: