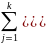4. Задача нахождения среднего времени и дисперсии времени перехода системы обслуживания
Задача нахождения среднего времени и дисперсии времени перехода системы обслуживания из одного состояния в другое сводится к построению по заданному алгоритму работы системы графа, получению его функции передачи с помощью правил преобразования графа и вычислению первой и второй производной от этой функции.
Однако нахождение ФП графа, а затем ее первой и второй производных, представляет собой очень трудоемкую задачу при сложном графе и су- щественно затрудняет анализ сложных алгоритмов работы систем обслужи- вания. Для упрощения анализа получим правила непосредственного нахож- дения среднего времени и дисперсии времени перехода из какой-либо на- чальной вершины составного графа до какой-либо конечной его вершины по известным средним временам перехода и дисперсиям времени перехода по составляющим этот граф элементарным дугам, без нахождения ФП составно- го графа, ее первой и второй производных .
Последовательный граф, параллельный граф, петля являются обра- зующими любого графа. То есть любой сложный граф состоит из графов пе- речисленных типов. Следовательно, достаточно получить правила нахожде- ния среднего времени и дисперсии времени перехода по образующим гра- фам, если известны среднее время и дисперсия перехода по составляющим эти графы дугам. С этой целью рассмотрим каждый образующий граф в от- дельности.
5. Последовательный граф
ФП такого графа от первой вершины до N-й, равна, произведению ФП составляющих дуг:
Ф1,N
s
s
Сначала рассмотрим граф, состоящий из двух последовательно соединенных дуг с ФП. Средние времена перехода от 1-й вершины до 2-й и от 2-й до 3-й вычисляются как
1,2=
- 
;
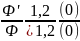2,3=
- 
.
Соответствующая этим временам дисперсия вычисляется как
21,2=
-
21,2;
22,3=
-
22,3.
Найдем среднее время перехода по рассматриваемому последовательному графу:
1,3=
=
=
.
Откуда следует:
1,3=
1,2
2,3.
Дисперсия времени перехода по рассматриваемому последовательному графу будет равна
21,3= + + 2 -﴾ - - ﴿2 =
1,2)2﴿
+
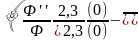2,3)2﴿
=
21,2
+
22,3.
Полученные формулы для последовательного графа, состоящего из двух дуг, нетрудно обобщить на случай, когда последовательный граф состоит из N -1 дуг. В результате такого обобщения найдем, что среднее время перехода по графу, состоящему из последовательности дуг N -1, находится как
1,N
=
i,i+1
,
а дисперсия времени перехода как
21,N
=
2i,i+1.
6. Параллельный граф
ФП параллельного графа равна сумме ФП егосоставляющих: k
Ф1,2(s) =
1,2,j
(s) ,
Где Ф1,2,j(s) – функция передачи от 1-ой вершины до 2-й по j-ой дуге.
1,2=
-
=-
=
Дисперсия будет иметь вид:
σ21,2==
-
21,2.
= σ21,2,j
+
21,2,j.
σ21,2==
-
21,2.
Как и в предыдущем случае, формулы нетрудно обобщить на многомерный случай. В результате такого обобщения получим следующие выражения:
1,2=
σ21,2=