Методические указания.
Построение линии пересечения поверхностей двух многогранников заключается в нахождении точек пересечения ребер одного многогранника с гранями второго и затем в нахождении точек пересечения ребер второго многогранника с гранями первого .
После нахождения точек перелома пространственной линии пересечения их нужно правильно соединить. Для этого можно воспользоваться схемой проф. Ананова. Выполняют условные развертки многогранников и накладывают их друг на друга (см. рис. 7). Если выполняется частичное пересечение многогранников, то построение условных разверток начинают с ребер, не участвующих в пересечении (на примере ребро С – призмы и ребро L – пирамида). Определяют точки пересечения многогранников на схеме. Например, точка I лежит на ребре К пирамиды и принадлежит грани АС призмы, соответственно ее обозначают на схеме и т.д. Соединять полученные точки на схеме можно только в пределах одной грани. На схеме Ананова можно определить видимость участков линии пересечения многогранников. Для этого схема Ананова строится для каждой плоскости проекций, потому что видимость многогранников на плоскостях проекций различна. В нашем примере видимость линии пересечения нужно определить только на фронтальной плоскости проекций. У призмы невидима грань АС, а у пирамиды грань МК. Заштриховываем эти грани на схеме Ананова. Участки линии пересечения, лежащие в заштрихованных зонах, невидмы.
Строим аксонометрическую проекцию одного из многогранников: а) выбираем положение осей аксонометрии на комплексном чертеже; б) определяем натуральные координаты точек по комплексному чертежу; в) определяем аксонометрические координаты этих точек; г) аксонометрические координаты откладываем по соответствующим осям.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.
Как строится линия взаимного пересечения многогранников?
Для чего применяется схема Ананова и ее суть?
Порядок построения аксонометрии?
Р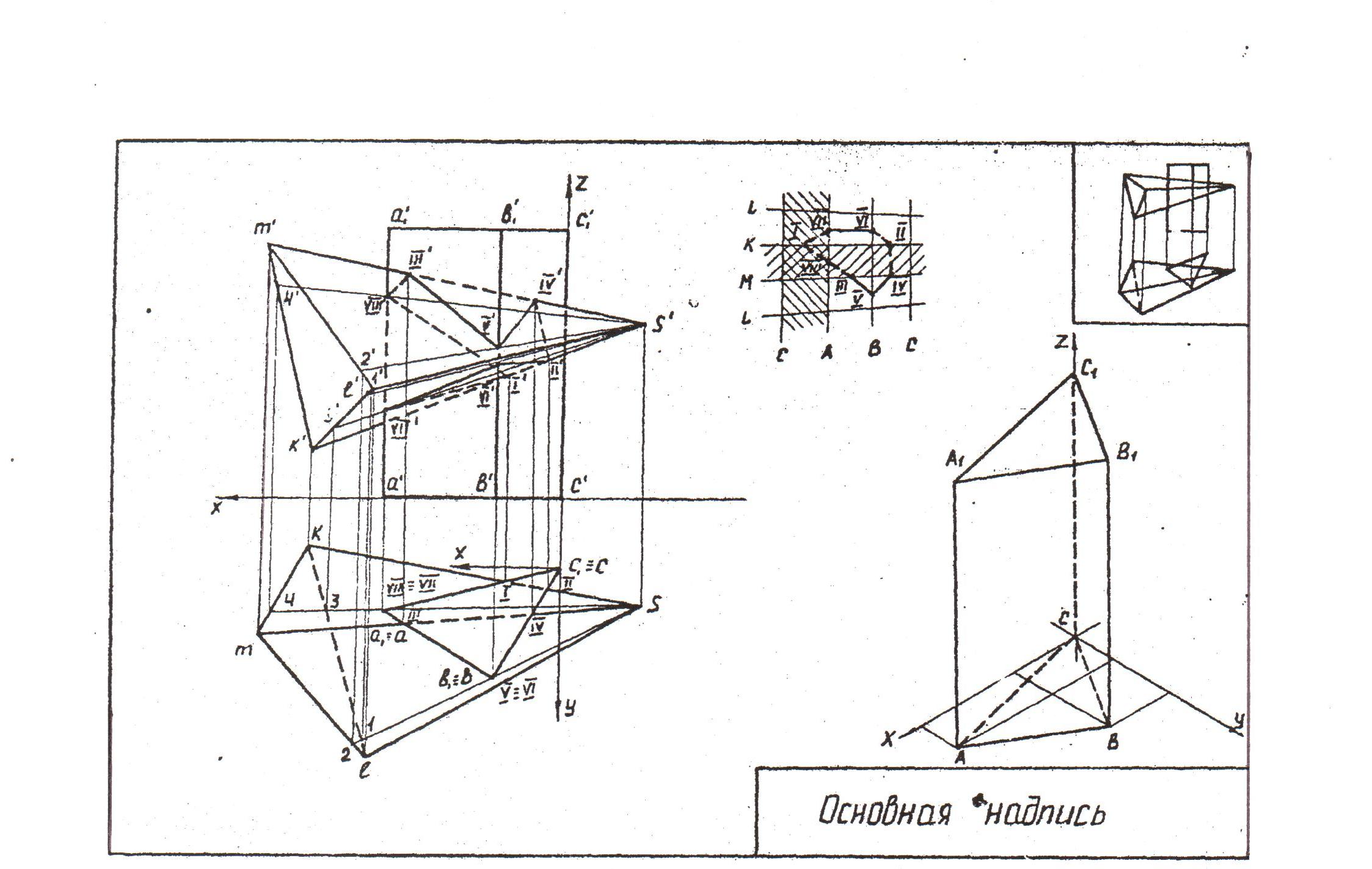
ис.7
Т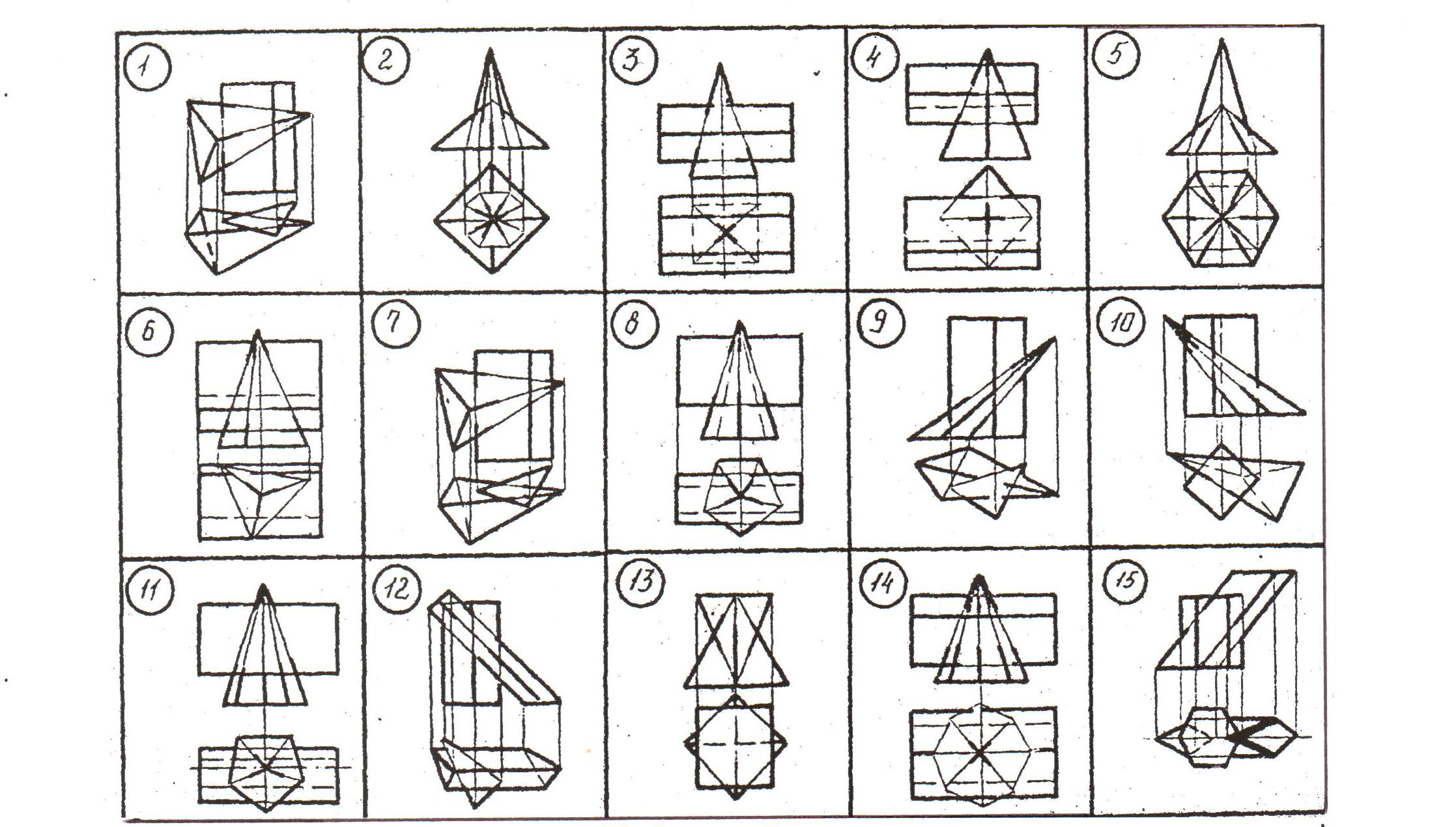
аблица
5
П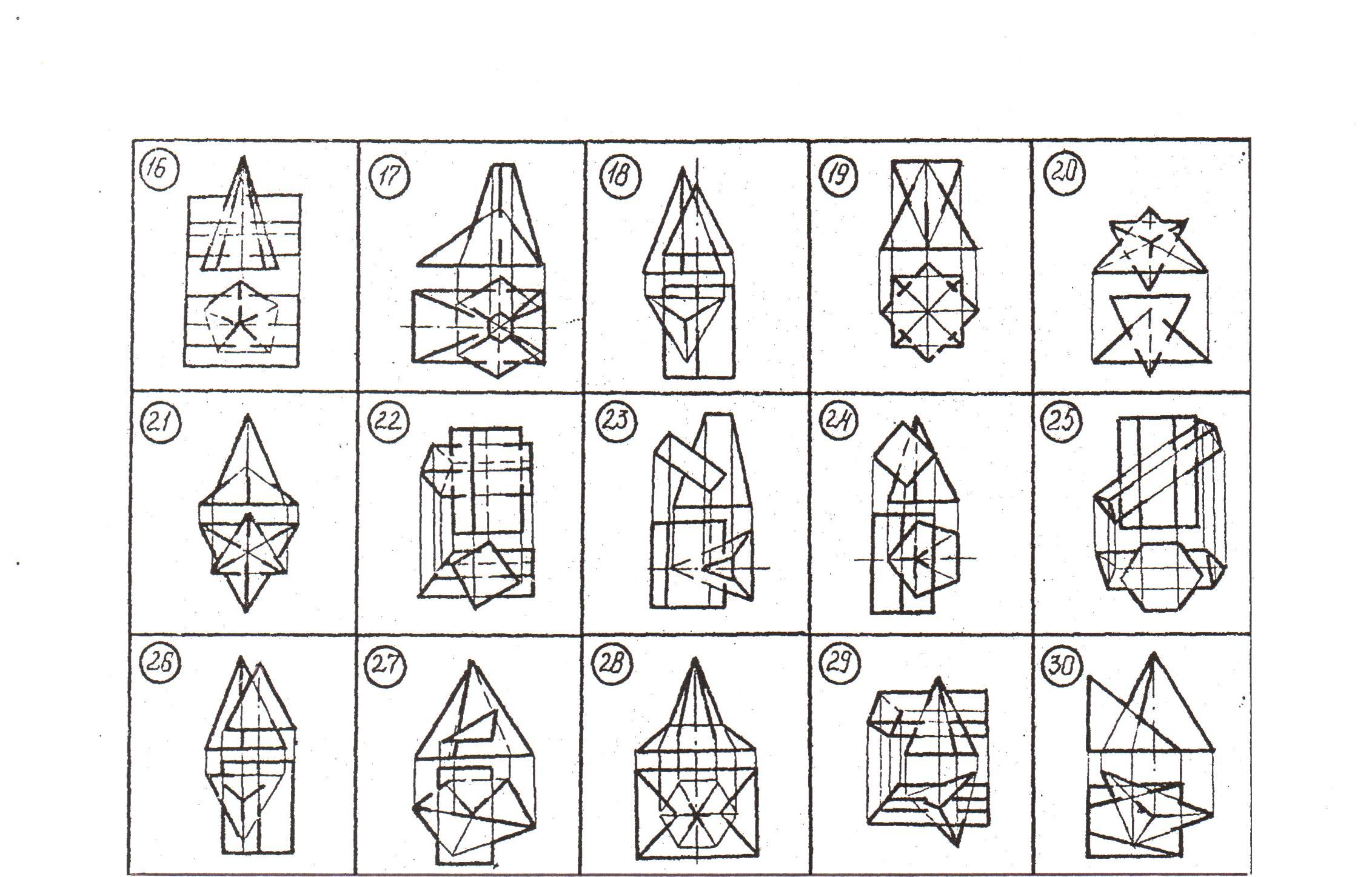
родолжение
таблицы 5
ЗАДАНИЕ № 6.
ТЕМА: Пересечение поверхностей.
ЦЕЛЬ ЗАДАНИЯ. Закрепление знаний и умений по построению линий взаимного пересечения поверхностей.
СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ЗАДАНИЯ. Построить линию взаимного пересечения двух поверхностей. Показать видимость на обеих проекциях. Пример выполнения задания дан на рис. 8. Данные для выполнения задания взять из таблицы 6.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ.
Для нахождения точек линии пересечения двух поверхностей применяют вспомогательные секущие плоскости, параллельные плоскостям проекции , вспомогательные секущие сферы , которые в пересечении с данными поверхностями могут дать простые линии пересечения (прямые, окружности). Сначала строят характерные или опорные точки искомой пространственной кривой. К ним относятся:
а) точки, проекции которых лежат на проекциях контурных линий поверхностей; б) точки, определяющие видимую часть линии пересечения от невидимой; в) «крайние точки» - правые и левые, высшие и низшие, ближайшие и наиболее удаленные от плоскостей проекций.
При взаимном пересечении многогранника с цилиндром, конусом или шаром участки кривой взаимного пересечения являются участками кривых второго порядка – окружности, эллипса, параболы и гиперболы. Построение надо начинать с нахождения точек пересечения ребер многогранника с кривой поверхностью.
Определить видимость линии пересечения, руководствуясь при этом следующим правилом: точка пересечения двух видимых линий при проецировании на какую-либо плоскость проекций - видима, точка пересечения двух невидимых или одной видимой и другой невидимой линии – невидима.