Федеральное бюджетное государственное образовательное учреждение

высшего профессионального образования

«Хакасский государственный университет им. Н.Ф.Катанова»

Инженерно-технический факультет

Расчетно-графические задания по

начертательной геометрии

для студентов 1 курса очной формы обучения

специальности 280700.62 Техносферная безопасность

2012

ВВЕДЕНИЕ

Начертательная геометрия является теоретическим обоснованием инженерной графики , дающей графическую подготовку к изучению последующих технических и специальных дисциплин.

Основными задачами изучения дисциплины являются:

• развитие у студентов пространственного мышления и навыков конструктивно-геометрического моделирования; выработка способностей к анализу и синтезу пространственных форм, реализуемых в виде чертежей зданий и сооружений;

• получение студентами знаний, умений и навыков по выполнению и чтению различных архитектурно-строительных и инженерно-технических чертежей зданий, сооружений, конструкций и их деталей и по составлению проектно-конструкторской и технической документации;

• изучение принципов и технологии моделирования двухмерного графического объекта (с элементами сборки); освоение методов и средств компьютеризации при работе с пакетами прикладных графических программ; изучение принципов и технологии получения конструкторской документации с помощью графических пакетов.

Изучение курса начертательной геометрии включает самостоятельную работу студентов с учебником, решение задач в рабочей тетради и выполнение расчетно-графической работы.

Расчетно-графическая работа по начертательной геометрии включает следующие задания (выполняемые на шести листах):

1. Взаимное положение плоскостей, прямой и плоскости.

2. Исследование многогранника с применением способов преобразования чертежа.

3. Сечение многогранника плоскостью и построения ее развертки.

4. Сечение кривой поверхности плоскостью и построение ее развертки.

5. Взаимное пересечение поверхностей многогранников.

6. Пересечение кривых поверхностей между собой или с многогранниками.

Прежде чем выполнять задания нужно изучить материал по данной теме и ознакомиться с решением задач, указанных в методических указаниях.

Чертежи должны быть выполнены в соответствии с ГОСТ Единой системы конструкторской документации (ЕСКД).

1. Задания выполняют на листах чертежной бумаги формата А3 (297х420).

2. Рамку чертежа наносят на расстоянии 5 мм от верхней, нижней и правой стороны формата. С левой стороны оставляют поле шириной 20 мм для подшивки чертежей.

3. В правом нижнем углу располагают основную надпись чертежа ГОСТ 2.104-68 (СТ СЭВ 368-76) (см. рис. 1)

В графах основной надписи записывают:

1 – индекс ХГУ НГ 0000000, что означает:

НГ – начертательная геометрия,

00 – номер темы,

00 – номер варианта,

000 – номер листа.

Например: ХГУ НГ 0118001 – цифровые обозначения расшифровываются следующим образом: первая тема, восемнадцатый вариант, первый лист.

2 – название темы задания,

3 – наименование кафедры,

4 – шифр группы,

5 – фамилия студента,

6 – фамилия преподавателя,

7,8 – подписи студента и преподавателя,

9 – дата выполнения работы,

10 – дата сдачи работы,

11 – масштаб выполнения задания,

12 – литера чертежа «У» (учебный чертеж).

4. Построение выполняют при помощи чертежных инструментов карандашом в тонких линиях. После проверки условия задачи обводят карандашом ТМ или М, а искомые линии красным карандашом. Толщина линий условия заданий и искомых 0,6-0,1 мм, осевых и линий построения 0,2-0,3 мм.

5. В правом верхнем углу чертежа пишется или вычерчивается условие задания.

6. Все записи на поле чертежа и в основной надписи выполняются чертежным шрифтом 3,5 и 5 ГОСТ 2,3С 4-68 (СТ СЭВ 851-78).

7. Задания выполняются, как правило, в двух проекциях фронтальной и горизонтальной.

8. Варианты заданий должны соответствовать порядковому номеру фамилии студента в списке группы.

9. Все чертежи контрольной работы подшиваются в альбом. Образец титульного листа прилагается (см. рис.2).

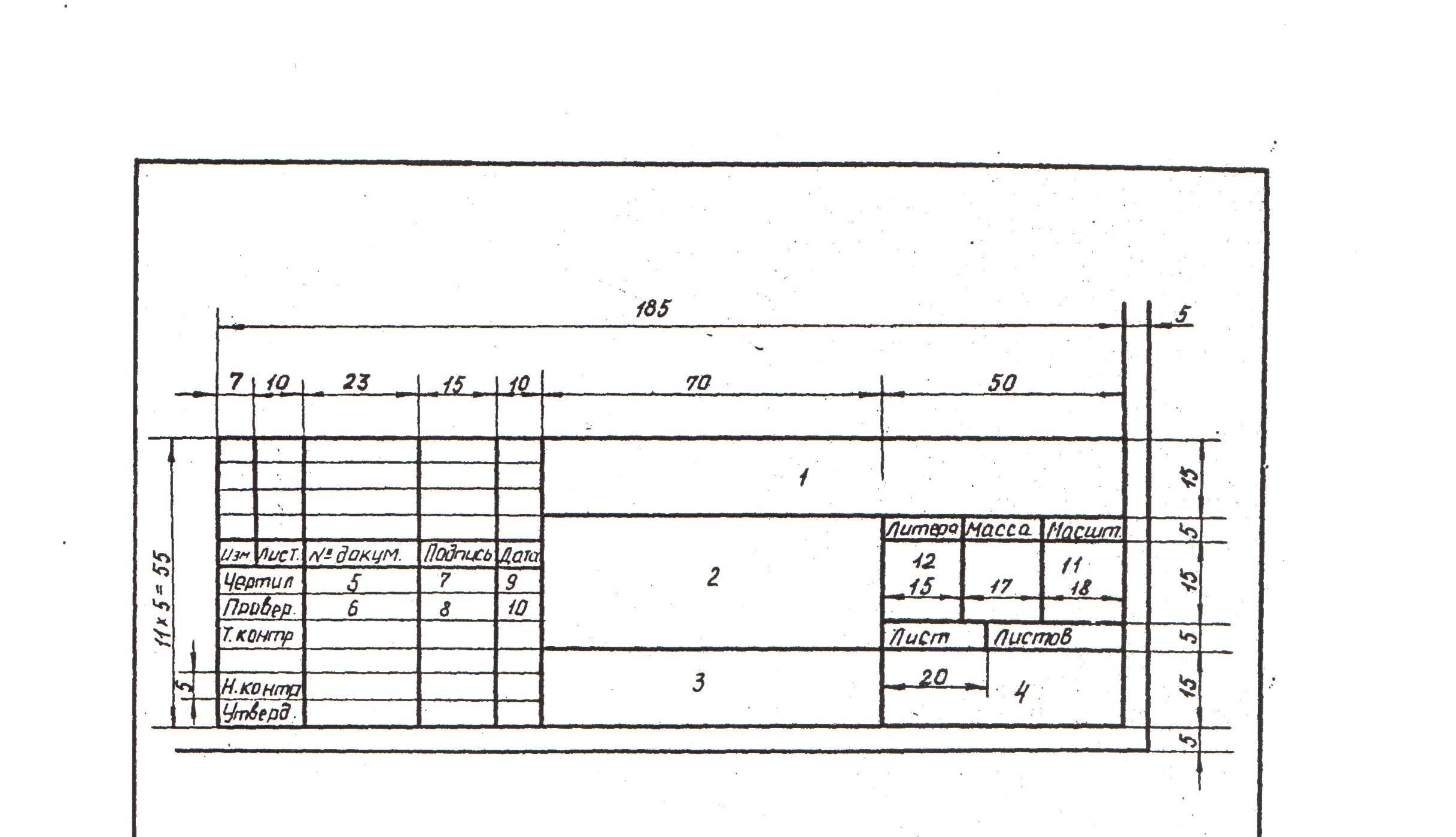
Рис.1.

ХАКАССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМ. Н.Ф. КАТАНОВА (ХГУ им. Н.Ф. Катанова)	№7
Кафедра городского строительства и хозяйства	№5
А Л Ь Б О М	№14
РАСЧЕТНО-ГРАФИЧЕСКИХ ЗАДАНИЙ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ	№7
Выполнил студент _________________________________________ (ФИО)	№7
___________________________________________________________	№7
Проверил __________________________________________________ (ФИО)	№7
Абакан	№5

рис. 2

Задание № 1. Тема: Взаимное положение плоскостей.

ЦЕЛЬ ЗАДАНИЯ: закрепление знаний и умений в решении задач на взаимное расположение плоскостей.

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ЗАДАНИЯ. Дана плоскость треугольника АВС и точка Д, требуется:

1. Определить расстояние от точки Д до плоскости, заданной треугольником АВС.

2. Построить плоскость, параллельную плоскости, заданной треугольником АВС, и отстоящую от нее на 35 мм.

3. Через вершину в треугольнике АВС построить линию ее пересечения с плоскостью, заданной треугольником АВС.

Пример выполнения задания дан на рис.3. Данные для выполнения задания взять из таблицы 1.

Методические указания.

Задачи 1 и 2 выполнить на чертеже в масштабе 2:1, (задачу 3 – в масштабе 2:1).

Выполнить разбивку листа, согласно, образца рис. 3.

1. Ход решения.

   • восстановить перпендикуляр к плоскости, заданной треугольником АВС, из данной точки Д.

   • определить точку пересечения этого перпендикуляра с плоскостью треугольника АВС.

   • определить натуральную величину отрезка перпендикуляра ДК, представляющего собой искомое расстояние.

2. Ход решения.

• взять произвольную точку в плоскости треугольника АВС, например, одну из вершин треугольника точку А, восстановить перпендикуляр в этой точке к плоскости, заданной треугольником АВС.

• выбрать на этом перпендикуляре произвольную точку Е и найти натуральную величину отрезка АЕ,

• отложить на натуральной величине от точки А заданное расстояние 35 мм, измеряемое отрезком АМ и найти проекции точки М,

• через точку М провести искомую плоскость, исходя из условий параллельности двух плоскостей.

3.Ход решения.

• определить искомую плоскость, перпендикулярную к АС, горизонтальную и фронтальную этой плоскости. перезадать искомую плоскость треугольником ВЕF, ограничив горизонталь и фронталь точками F и Е,

• найти линию пересечения двух плоскостей , заданных треугольниками АВС и ВЕ.

• установить видимость треугольников на плоскостях проекций с помощью конкурирующих точек.

Вопросы для самопроверки.

1. Что называется горизонталью плоскости?

2. Как провести горизонталь в плоскости общего положения, заданной треугольником? фронталь? профильную прямую?

3. Как располагается на комплексном чертеже проекция прямой, перпендикулярной к плоскости?

4. Как определить расстояние от точки до плоскости общего положения?

5. Какие плоскости обычно применяются в качестве вспомогательных при определении точки встречи прямой с плоскостью?

6. Из каких задач состоит построение точки пересечения прямой с плоскостью?

7. Как провести плоскость, параллельную данной плоскости?

8. Как построить взаимно перпендикулярные плоскости?

Рис. 3

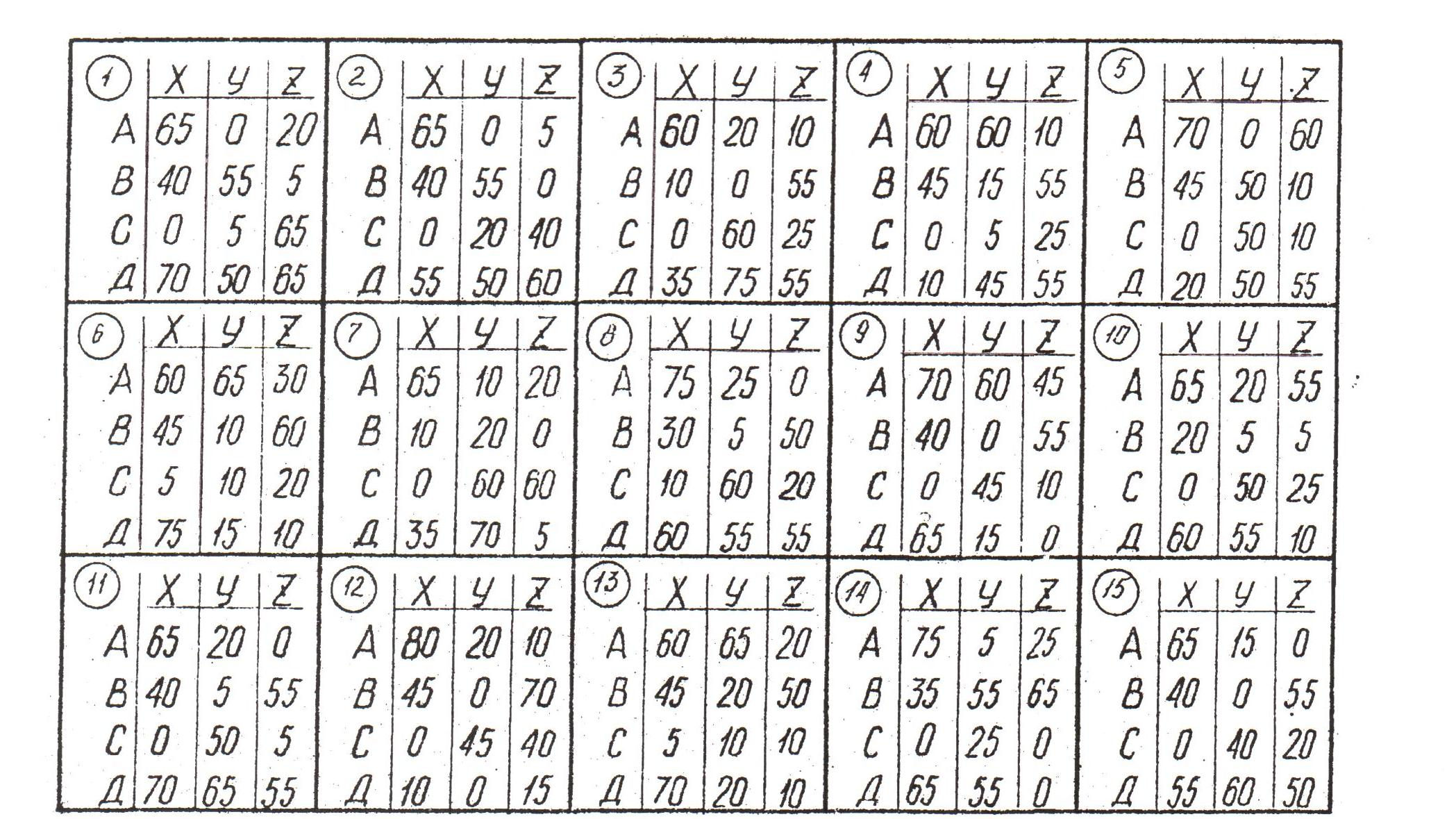
Таблица 1.

П родолжение таблицы 1. Задание № 2. Тема: Исследование многогранника с применением способов преобразование чертежа.

ЦЕЛЬ ЗАДАНИЯ: закрепление знаний и умений о способах преобразования комплексного чертежа.

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ЗАДАНИЯ. Дан неправильный многогранник. Определить натуральную величину:

1. расстояние между указанными параллельными ребрами;

2. кратчайшего расстояния между указанными скрещивающимися ребрами;

3. расстояния от вершины до ребра или грани;

4. расстояние от ребра до параллельной ему грани;

5. двугранного угла между гранями многогранника.

Пример выполнения задания дан на рис. 4. Данные для выполнения задания взять из таблицы 2.