Марковские цепи дискретного времени

Более продвинутым вариантом табличной логики и конечных автоматов являются Марковские цепи. При достаточно детальной проработке данный метод позволяет компьютерным оппонентам строить прогнозы развития событий для любых игровых ситуаций, выдвигать собственные оценки и гипотезы насчёт дальнейшего их развития. Этот метод также хорош тем, что в сходных ситуациях ИИ всегда будет принимать сколько-нибудь различающиеся решения, что делает поведение управляемых им персонажей более живым и непредсказуемым.

Данный метод основан на оперировании таблицами вероятностей перехода из одного состояния в другое в каждый данный момент времени. Эта таблица или матрица вероятностей, в общем случае, будет иметь следующий вид:

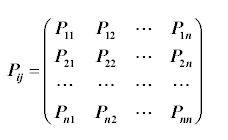
В каждый конкретный момент времени система находится в одном состоянии из набора заданных состояний P₁, P₂,…P_n . Переход из текущего состояния в любое другое, доступное для перехода, осуществляется скачкообразно, мгновенно. В каждый момент времени этот переход может быть осуществлён с заданной по таблице вероятностью.

Сама таблица выглядит так:

	S1	S2	...	Sn
S1	P11	P12	...	P1n
S2	P21	P22	...	P2n
...	...	...	...	...
Sт	Pn1	Pn2	...	Pnn

Строки здесь соответствуют состояниям системы S₁…S_n, в которых система может находиться (или уже находится) в текущий момент времени, а столбцы – состояниям, в которые система может перейти. На пересечении строки с номером i и столбца с номером j располагается P_ij - вероятность перехода из состояния S_i в состояние S_j.

Рассмотрим более подробно реализацию метода на примере несложной практической задачи:

Персонаж, управляемый компьютерным оппонентом, производит по движущейся цели несколько выстрелов подряд. Необходимо определить, какие повреждения цель, вероятнее всего, получит по результатам четырёх последовательных выстрелов.

Для простоты скажем, что цель может находиться в четырёх состояниях (каждому из состояний, на практике, можно поставить в соответствие определённый процент «очков прочности», хит-поинтов цели):

S₁ - цель невредима;

S₂ - лёгкие повреждения;

S₃ - значительные повреждения;

S₄ - цель полностью уничтожена.

Повреждения, наносимые цели каждым выстрелом, зависят от ряда условий, которые будем считать случайными; одно любое «удачное» попадание способно полностью уничтожить даже совершенно невредимую цель. Промах же, соответственно, никак не изменит состояние цели. В начальный момент времени цель находится в состоянии S₁.

Изобразим, для наглядности, схему возможных переходов. Для простоты, не изображены условия промаха для каждого из состояний (вероятности P_ij и стрелки, началом и концом которых является одно и то же состояние).

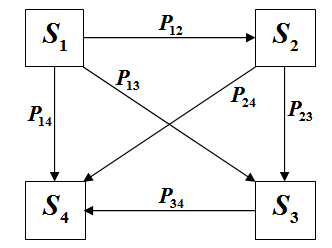
Запишем, в соответствие со схемой, матрицу вероятностей переходов, заполнив её приблизительными значениями вероятностей для каждого из вариантов. Будем считать, что вероятности здесь соотносятся с точностью стреляющего, с маневренными свойствами цели и рядом других подобных параметров:

Так как известно, что на момент начала стрельбы цель была невредима, то вероятности нахождения системы в состояниях S₁…S₄ до стрельбы можно записать как: P₁(0)=1, P₂(0)=0, P₃(0)=0, P₄(0)=0.

После первого выстрела эти вероятности, очевидно, изменятся. Из состояния S₁ могло произойти 4 перехода – в состояние S₁ (промах), в S₂ (лёгкие повреждения), в S₃ (тяжёлые повреждения) и в S₄ (цель уничтожена). Этим переходам соответствует первая строка матрицы, а сами вероятности нахождения цели в состояниях S₁… S₄ будут иметь после выстрела следующие значения: P₁(1)=0.3, P₂(1)=0.4, P₃(1)=0.2, P₄(1)=0.1.

Перед вторым выстрелом цель может с некоторой долей вероятности находиться в любом из четырёх состояний. Значит, для оценки “результатов” второго выстрела следует рассмотреть все возможные случаи. Воспользуемся формулой для условных вероятностей.

Так, по результатам двух выстрелов цель может (например) иметь тяжёлые повреждения. Это могло произойти тремя различными способами:

1. Первый выстрел – промах, второй – тяжёлые повреждения.

2. Первый выстрел – лёгкие повреждения, второй – тяжёлые.

3. Первый выстрел – тяжёлые повреждения, второй – промах.

Для того чтобы получить значение искомой величины, и используются условные вероятности. Иначе говоря, вероятность получения целью тяжёлых повреждений рассчитывается как сумма вероятностей всех возможных переходов в состояние S₃ при условии, что цель уже пребывает в состоянии, предшествующем переходу:

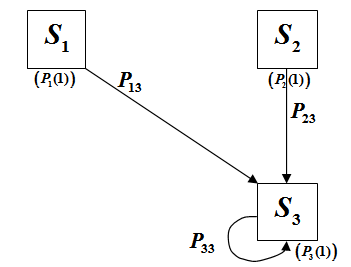
Тогда P₃(2) можно рассчитать как:

P₃(2) = P₁(1)* P₁₃ + P₂(1)* P₂₃ + P₃(1)* P₃₃ = 0.3*0.2+0.4*0.4+0.2*0.3=0.28

Проведя аналогичные вычисления для оставшихся состояний, получим:

P₁(2) = 0.09; P₂(2) = 0.28; P₃(2) = 0.28; P₄(2) = 0.35;

(сумма всех четырёх вероятностей должна равняться единице – это значит, что нет неучтённых возможностей)

Для третьего выстрела расчёт проводится таким же образом, что и для второго, однако, тут, в качестве вероятностей пребывания в исходных(до перехода) состояниях следует использовать вероятности, полученные на прошлом шаге (т.е. для состояния после второго выстрела). Отсюда:

P₁(3) = 0.027; P₂(3) = 0.148; P₃(3) = 0.214; P₄(3) = 0.611;

Так, после четвёртого выстрела:

P₁(4) = 0.0081; P₂(4) = 0.07; P₃(4) = 0.1288; P₄(4) = 0.7931;

В результате, после четвёртого выстрела вероятность уничтожения цели приблизилась к 80%. Можно сказать, что в 4 случаях из 5 цель будет полностью уничтожена, а вероятность того, что ни один из выстрелов не достиг цели, будет менее процента.

Подобный подход позволяет создавать отдельные подсистемы ИИ, отвечающие за оценку событий, принятие решений и формулирование управляющих выводов. К примеру, компьютерный оппонент, реализующий подобную схему, может перед боем оценивать вероятность уничтожения игрока имеющимся вооружением раньше, чем игрок уничтожит его, и принимать решение занять оборону или отступить в целях перегруппировки.

Произведя несколько выстрелов, он может, вычислив вероятность вывода из строя игрока различными способами (с учётом свойств ландшафта и окружения, если требуется), применить наиболее действенный для данной ситуации. ИИ может, не зная точного маршрута передвижений игрока, выдвигать несколько “гипотез”, и, основываясь на сведениях о последних точках, где игрок был замечен, вычислять наиболее вероятный маршрут. При этом, что важно, игрок может запутывать преследователей, используя отвлекающие манёвры, уловки - и ИИ, подобно человеку, пойдёт по ложному следу. Словом, подобные приёмы способны сделать поведение персонажей под управлением компьютерного оппонента гораздо более живым, интересным и правдоподобным.

Кроме того, возможно использование Марковских цепей дискретного времени и на этапе проработки игровой механики – составляя и верно применяя матрицы вероятностей, можно оценить результаты того или иного взаимодействия между объектами игрового мира. Это способно значительно сократить усилия и время на дальнейшую «шлифовку» и доводку игрового процесса.

Схемы на основе Марковских цепей – мощное, но недооцененное средство с широкими возможностями для реализации элементов искусственного интеллекта.

18