10) Идеальный емкостный элемент в цепи синусоидального тока

Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение , то ток i  через него будет равен 

.

(3)

 

П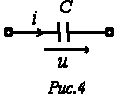 олученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на /2

Введенный параметр называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, имеет размерность Ом. Однако в отличие от Rданный параметр является функцией частоты

11)Цепь синусоидального тока с последовательным соединением элементов. Топографическая диаграмма напряжений

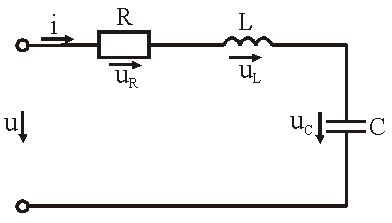Рис. 3.7 – Схема замещения последовательной цепи R, L, C

Для последовательной цепи общим является ток. Согласно второму закону Кирхгофа для мгновенных значений напряжение на входе цепи определяется выражением

u = u_R + u_L + u_C.

Запишем это уравнение в комплексной форме

U = U_R + U_L + U_C.

Построение векторной диаграммы начинаем с отложения на комплексной плоскости вектора тока I, который является общим для всех элементов цепи. Причём направление вектора выбираем произвольно. Вектор напряжения на активном сопротивлении U_R совпадает по направлению с вектором тока, его называют активной составляющей напряжения, U_R = R∙I. Вектор напряжения на индуктивности катушки U_L = jX_L∙I опережает вектор тока на угол 90°. Вектор напряжения на ёмкости U_C = - jX_C∙I отстаёт от вектора тока на угол 90°.

Геометрическая сумма трех векторов напряжения даёт вектор напряжения U, приложенного к цепи. Результирующий вектор напряжения U опережает вектор тока I на угол φ.

При построении диаграммы условно принято U_L > U_C. В построенной диаграмме можно выделить треугольник ОАВ, называемый треугольником напряжений. Сторона треугольника

АВ = U_Х = U_L + U_C = j(X_L – X_C)·I

называется реактивной составляющей напряжения. Из треугольника напряжений можно найти модуль напряжения на зажимах в цепи

Заменяя напряжения на элементах произведением тока на соответствующие сопротивления, получаем

U = R·I + jX_L·I – jX_C · I = I·[R + j(X_L – X_C)] = Z·I,

где Z – полное комплексное сопротивление цепи,

Z = R + j(X_L – X_C).

Разделим все векторы комплексных напряжений (треугольника ОАВ, рис. 3.8, а) на вектор комплексного тока, тогда получим треугольник сопротивления О'А'В' для случая X_L>X_C . Из треугольника сопротивлений можно определить модуль полного сопротивления и угол φ

Знак угла φ зависит от характера нагрузки: плюс соответствует индуктивной нагрузке, минус – ёмкостной.

В общем случае электрическая цепь в зависимости от соотношения между индуктивным и емкостным сопротивлениями может иметь индуктивный характер при X_L > X_C, емкостный характер при X_L < X_C и активный характер при X_L = X_C.

12)Цепь синусоидального тока с параллельным соединением элементов. Топографическая диаграмма напряжений

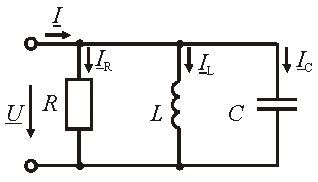Рис. 3.10 – Схема замещения параллельной цепи R, L, C

где комплексные сопротивления ветвей соответственно равны

Z₁ = R₁, Z₂ = jωL = jX_L, Z₃ = - j1/ωC = - jX_C.

Общий ток согласно первого закона Кирхгофа

I = I_R + I_L + I_C.

Вектор тока I_R совпадает по фазе с напряжением; вектор тока I_L через индуктивность отстает от напряжения на угол 90°; вектор тока I_С через ёмкость опережает напряжение на угол 90°. Условно принимаем, что I_L<I_С.

Геометрическая сумма трех векторов токов I_R, I_L, I_С даёт вектор тока в неразветвлённый части цепи. Этот вектор I опережает вектор приложенного к цепи напряжения на угол φ. В этом случае говорят об ёмкостном характере нагрузки в цепи. В построенной диаграмме можно выделить треугольник ОАВ, называемый треугольником токов. Отдельно он показан на рис. 3.11, б. Сторона О₁В₁ называется активной составляющей тока, сторона А₁В₁ – реактивной составляющей тока. Из треугольника токов получаем модуль полного тока

где

I_Х = I_L + I_С.

Выражения для составляющих токов и угла φ

I_R = I·cosφ, I_X = I·sinφ,   .

активную проводимость , реактивную проводимость полную комплексную проводимость

у = g + jb,

а ее модуль