Исходные данные.

Вариант № 4.3 ( вертолёт–кран ).

Масса m, кг	Двигатели			Параметры НВ				Рулевой винт		Высота
	Тип	Число	Мощность одного двигателя N, кВт	Диаметр D, м	Число лопастей Kл	Заполнение σ7	Окружная скорость ωR, м/c	Диаметр Dрв, м	Расстояние от оси НВ Lрв, м	Вертолёта, м	Висения у земли H, м
35000	ТВД	2	4800	32	6	0,1	200	6	19.2	6,7	7,7

Тип лопастей НВ	Форма в плане	Относительная толщина профиля в сечениях лопастей	Профиль для всех типов лопастей
Лопасти стеклотекстолитовые	Прямоугольная ; ηл = 1

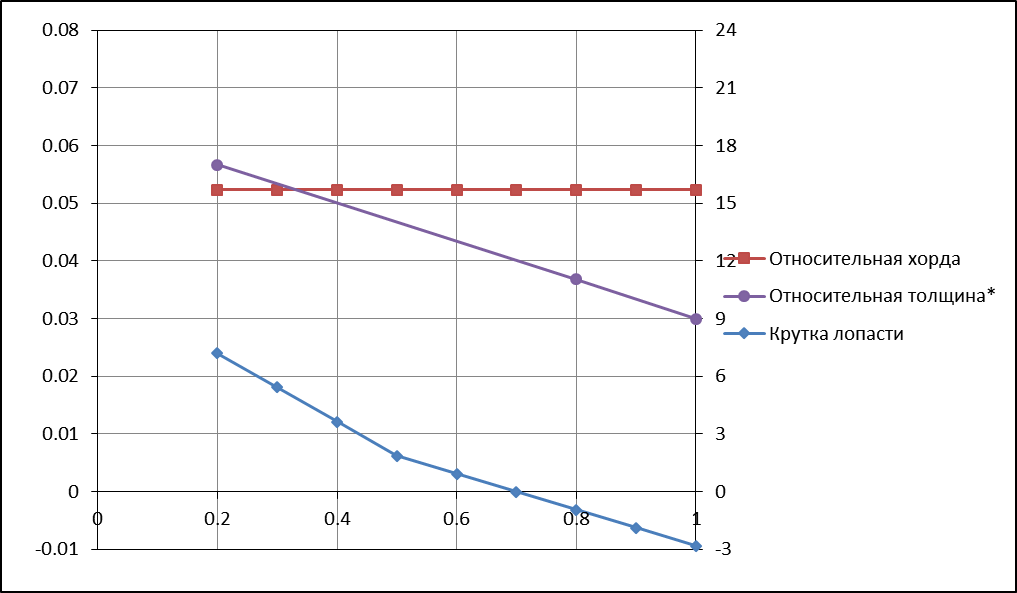
I. Геометрические характеристики лопастей несущего винта. Расчет крутки лопасти.

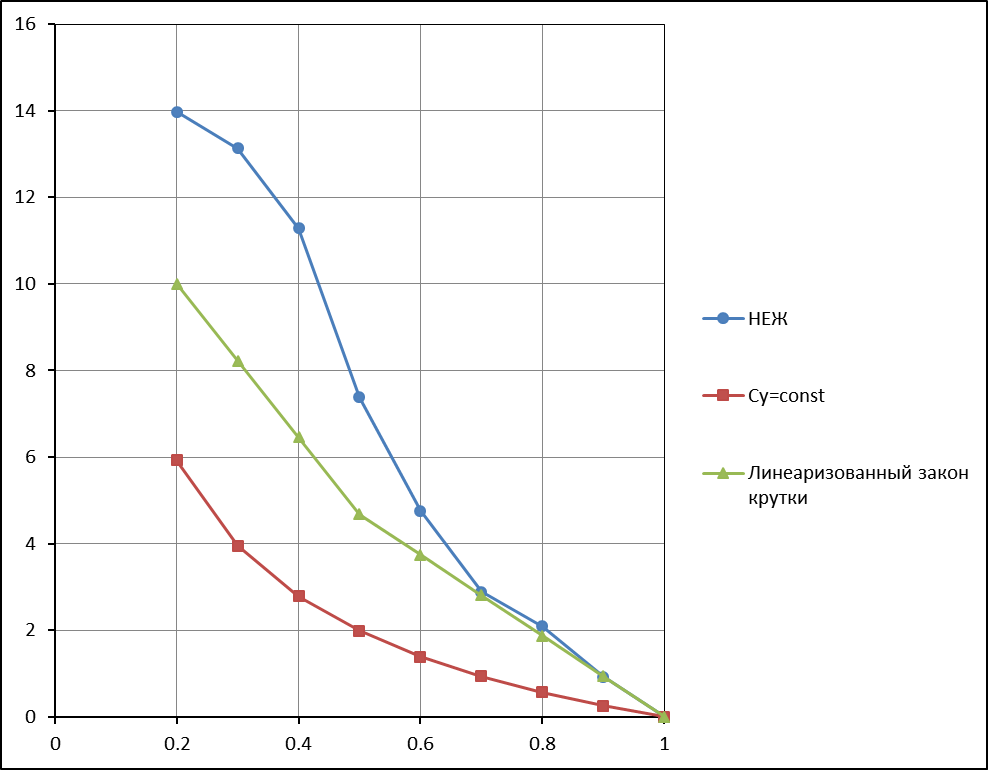
Цель расчёта – определить крутку лопасти, при которой относительный КПД винта имеет наибольшее значение. Расчёт производится для режима висения вертолёта у земли (H=0 м, ρ₀=1,266 кг/м³) без учёта сжимаемости воздуха. Минимальными индуктивными потерями обладает винт НЕЖ, а минимальными профильными потерями – винт с постоянным распределением по длине лопасти углов атаки сечений. Поэтому расчёт производится отдельно для этих двух случаев, и находятся законы крутки, обеспечивающие минимальные индуктивные и минимальные профильные сопротивления соответственно. Далее выбирается компромиссный закон крутки, обеспечивающий максимальный относительный КПД винта. Этот закон крутки должен отвечать не только аэродинамическим требованиям, но и конструктивно–технологическим. Исходя из этого, крутку целесообразно делать линейной.

Расчёт.

Вычисляем удельную нагрузку на площадь, ометаемую лопастями несущего винта:

Из таблицы выбираем значение коэффициента силы тяги , учитывающего форму лопасти в плане; для прямоугольной лопасти имеем:

Вычисляем коэффициент тяги винта:

Коэффициент концевых и втулочных потерь по приближённой формуле Б. Н. Юрьева:

Вычисляем значение коэффициента подъёмной силы профиля в характерном сечении:

1. Далее расчёт ведётся для винта с постоянным распределением по длине лопасти углов атаки.

2. Далее расчёт ведётся для компенсированного винта неж.

Определяется относительная индуктивная скорость, постоянная по длине лопасти

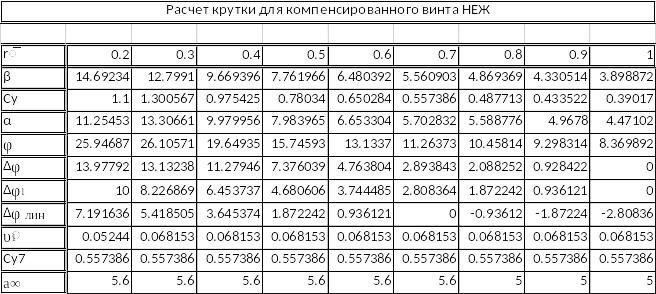
Абсолютное значение отрицательной крутки лопасти

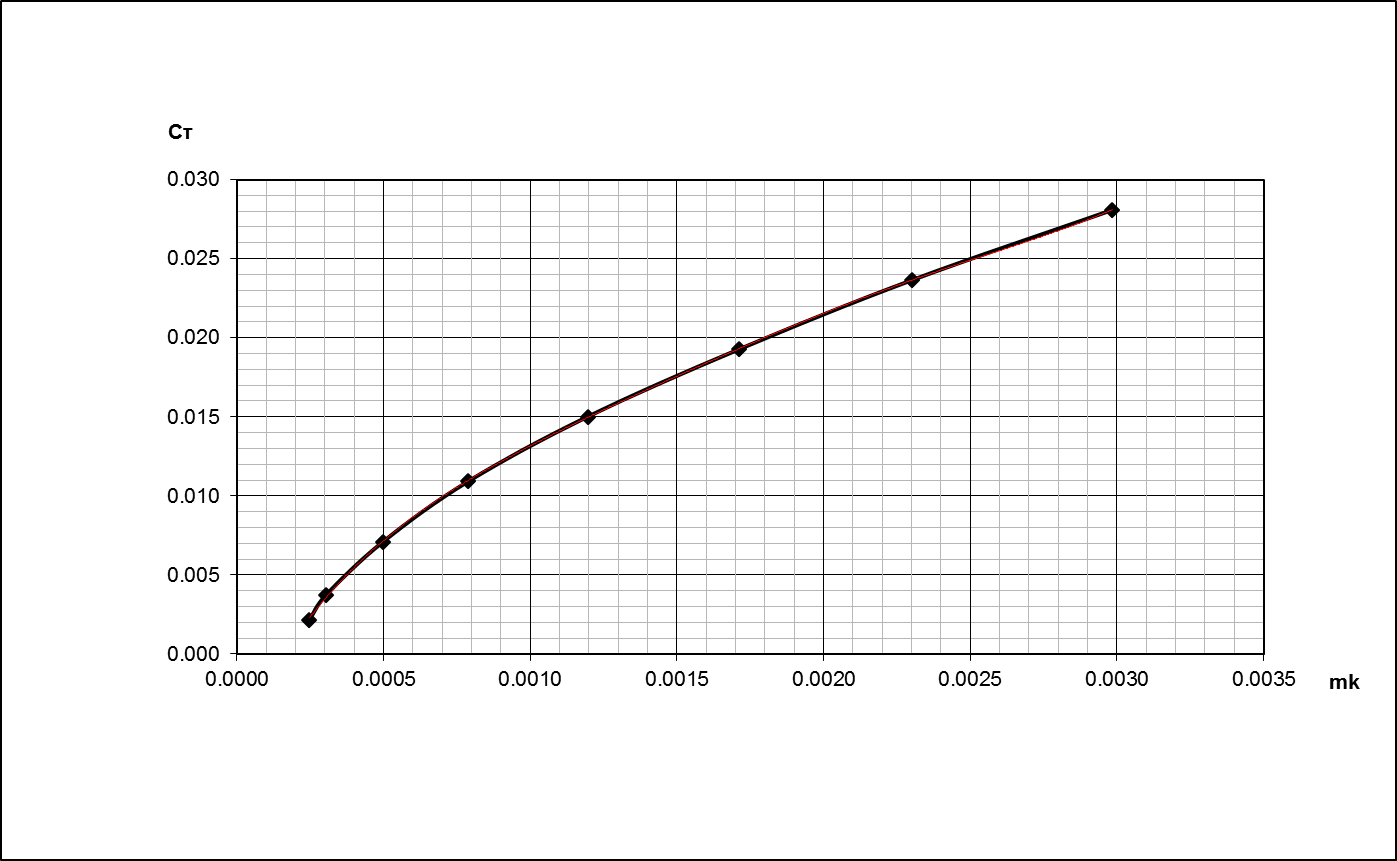
II. Расчёт поляры несущего винта на режиме висения.

Поляра несущего винта на режиме висения представляет собой зависимость

Для ряда значений угла установки вычисляются значения коэффициентов тяги и крутящего момента методом табличного интегрирования (метод трапеций). Подынтегральные функции выражаются следующим образом:

В записанных выражениях:

где

M – текущее число Маха

M_о – число Маха на конце лопасти,

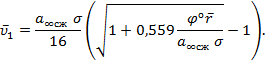
Размерность в вышеприведённых формулах . Расчёты ведутся для фиксированных значений угла установки и сводятся в таблицы. Участок относительных радиусов занят втулкой, размеры рукавов которой равны приблизительно а коэффициент их сопротивления Индуктивное сопротивление на этом участке отсутствует.

Вычисление коэффициента тяги ведётся по следующим формулам

где – условный радиус, на котором заканчиваются рабочие сечения лопасти. Приближённо полагается, что кончики лопастей не создают подъёмных сил из–за концевых потерь. B – коэффициент, учитывающий концевые потери

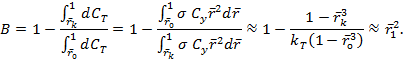
По Б.Н.Юрьеву:

где – число лопастей винта.

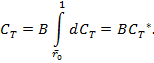
Здесь С_T^*– аэродинамический коэффициент силы тяги, вычисленный без учёта концевых потерь.

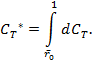
Значение коэффициента концевых потерь приближённо может быть вычислено через С_T^*, т.е.

Аэродинамический коэффициент крутящего момента вычисляется так:

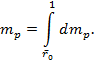
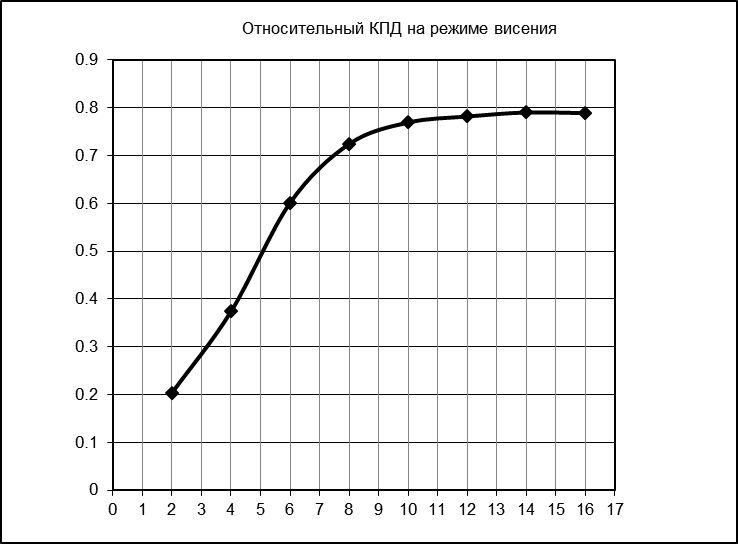
Расчёт выполняется для углов установки φ₇ = 2^о, 4^о, 6^о, 8^о, 10^о, 12^о, 14^о, 16^о и сводится в таблицы. На основании табличных данных методом трапеций вычисляются интегралы, строится поляра несущего винта для режима висения . Вычисляются значения относительного КПД винта:

строится зависимость