2.26. Прямая линия

Прямая линия в пространстве однозначно определяется точкой , через которую проходит и вектором , которому она коллинеарна.

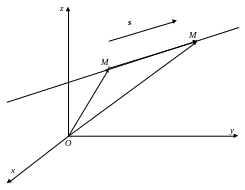
Из рисунка видно, что вектор и направляющий вектор s коллинеарны и отличаются числовым множителем t. Векторный треугольник дает

.

Таким образом, и векторное уравнение прямой принимает вид

(2.26.1)

Запишем векторное уравнение (2.26.1) в координатах

(2.26.2)

Система (2.26.2) называется – параметрические уравнения прямой линии.

Исключив из уравнений (2.26.2) параметр t, получим канонические уравнения прямой линии

(2.26.3)

Соотношения (2.26.3) представляют собой три уравнения. Если какое-либо из чисел m,n,p окажется равным нулю (например, m=0), это будет означать, что соответствующий числитель тоже равен нулю (в нашем случае ).

Если прямая проходит через две заданные точки и , то уравнением такой прямой будут соотношения

(2.26.4)

Если прямая (2.26.3) и плоскость перпендикулярны, то их коэффициенты удовлетворяют условию

(2.26.5)

Если прямая (2.26.3) и плоскость параллельны, то их коэффициенты удовлетворяют условию

(2.26.6)

Если прямая (2.26.3) и плоскость пересекаются, то их координаты точки пересечения находятся по формулам

(2.26.7)

В пространстве векторное уравнение прямой имеет тот же вид

(2.26.8)

Здесь .

Параметрические уравнения прямой записываются

(2.26.9)

Исключение параметра t дает канонические уравнения прямой

(2.26.10)

Из элементарной геометрии известно, что прямая линия является пересечением двух плоскостей. Поэтому система уравнений

(2.26.11)

тоже представляет некоторую прямую в пространстве. Система (2.26.11) называется – общие уравнения прямой.