Производная по направлению

Z=x³-3x³y+3xy²+1 и точки M(3;1) и М₁(6;5)

1. Находим l=(вектор)MM₁={3;4}

2. Находим длину |l|

3. l₀={ } где, x=cosα, y=cosβ

4. Находим первые производные и подставляем в место х и у значения точки M₀

5. И все найденное подставляем в формулу:

Нахождение ДИФФЕРЕНЦИАЛА.

1. Сначала находим производную

2. Затем придел производной

3. Потом и сам дифференциал

ФОРМУЛА ТЕЙЛОРА

ФОРМУЛА ТЕЙЛОРА ДЛЯ 3х ПЕРЕМЕННЫХ

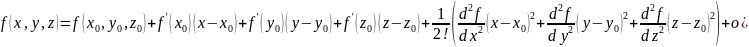
Где формула приращения

Третья частная производная (f’’’) для 2х переменных:

Где:

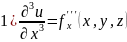
Вторая частная производная (f’’) для 2х переменных:

Эквивалентность Б.М и Б.Б.

Чтобы сравнить две бесконечно малые величины, нужно найти предел их отношений. И по таблице эквивалентности.

Производные первого порядка для неявно заданной функции:

Остаточный член форма Пеано

где M( ). Для формулы Тейлора

Непрерывность и диф-сть ФНП

Непрерывность:

Диф-ть: (зададим приращение)

Вычисление приближённо

Вычислим приближённо с помощью дифференциала

Производные высших порядков заданных параметрически

То производные последовательно могут быть вычислены по формулам:

и д.т.

Экстремумы трех переменных

1. Находим первые производные

2. Составляем систему уравнения

Выделяем

Подставляем х и у в систему находим соответствующие точки (х₁;у₁) и (х₂;у₂) т.е. М₁(х₁;у₁) и М₂(х₂;у₂)

3. Находим все вторые частные производные

15