Алгоритм Прима

Формулировка задачи. Дан взвешенный граф, в котором веса присвоены ребрам. Необходимо найти минимальное остовное дерево имеющую своим корнем одну из вершин графа.

 

Идея алгоритма. Пусть часть остовного дерева уже построена. Это утверждения всегда верно, так как в начале процесса вершина с которой начинается построение уже входит в дерево. Итак если часть основного дерева уже есть, то множество вершин графа можно разделить на два подмножества: подмножество состоящее из вершин уже построенного остовного дерева и оставшихся вершин графа.

Очевидно, что среди ребер соединяющихся эти два множества существует ребро наименьшего веса. Можно доказать, (но мы здесь этого делать не будем) что минимальное дерево проходит через это ребро.

 

Алгоритм.

 

        Множество остовных вершин – исходная веришны

        Множество оставшихся - все вершины за исключением исходной.

        Пока множество оставшихся не пусто

o       Ищем ребро соединяющее множество остовных и множество оставшихся и имеющее наименьший вес.

o       Для найденного ребра, вершину принадлежащую множеству оставшихся:

        Вычеркиваем из множества оставшихся.

        Добавляем к множеству остовных.

Определение структур

#define INF 1000000 // бесконечность

struct REBRO{

int v1,v2,Cost;

};

struct GRAPH{

int nVersh; // число вершин графа

int nReber; // числ ребер графа

int **m; // матрица смежности

bool *Included; // Included[i] - true, если i-я вершина уже включена в остов

int nOstovReber; // число ребер в остове

REBRO *OstovRebro; // ребра, принадлежащее остовному дереву

};

Implementation

// Предполагается, что все начальные установки в графе *gr выполнены

void PrimOstov(GRAPH *gr, int Start){

int i,j,ki,kj,MinCost,nIncluded=1,Cost;

bool b;

int nr=0; // число ребер в остовном дереве

gr->Included[Start]=true; // стартовая вершина включается в остовное дерево

nIncluded=1;

while(nIncluded<gr->nVersh){ // пока все вершины не будут включены

ki=0;

kj=0; // ki,kj - ребро будет ребром минимальной стоимости

MinCost=INF;

// ищем минимальное ребро, одна вершина которого

// уже входит в остовное

// дерево, а вторая ещё нет

for(i=0; i<gr->nVersh; i++){

if(gr->Included[i]){

for(j=0; j<gr->nVersh; j++){

b=!gr->Included[j];

Cost=gr->m[i][j];

if(b && Cost<MinCost){

ki=i;

kj=j;

MinCost=Cost;

} // if

} // for j

} // if(gr->Included[i])

} // for i

// включаем ребро в остовное дерево

gr->OstovRebro[nr].v1=ki;

gr->OstovRebro[nr].v2=kj;

gr->OstovRebro[nr].Cost=MinCost;

gr->Included[kj]=true;

nIncluded++;

nr++;

} // while

gr->nOstovReber=nr;

}

Алгоритм Краскала

Формулировка задачи. Дан взвешенный граф, в котором веса присвоены ребрам. Необходимо найти минимальное остовное дерево имеющую своим корнем одну из вершин графа.

 

Идея алгоритма. Искомые ребра соединяют вершины. Поэтому возможны две стратегии построения. Можно идти от вершин и для каждой из них искать минимальное ребро (как это сделано в алгоритме Прима) а можно для каждого ребра выяснять можно ли его включить в строящееся дерево. Алгоритм Краскала предлагает делать это следующим образом. Во-первых, ребра графа пронумеровываем в порядке возрастания весов. Затем для каждого ребра начиная с первого проверяем соединяет или нет оно две несвязные вершины, если да, то его можно включить в остовное дерево. Ясно, что если мы имеем V вершин, то работа алгоритма начинается с V несвязных компонент графа (пока из графа все ребра исключаем). Для того, чтобы их связать необходимо найти V-1 ребро.

Другими словами, алгоритм организует процесс роста компонент связности в процессе которого он объединяются друг с другом до тех пор пока не останется одна являющаяся конечным результатом.

 

Структуры данных. В алгоритме используется термин «компонента связности». Такой конструкции нет ни в одном языке программирования. Это исключительно математический термин, поэтому для конкретной реализации алгоритма необходимо тщательно продумать вопрос о представлении «компоненты связности» существующими языковыми конструкциями.

 

Алгоритм

 

1. Создаем список ребер по возрастанию.

2. Создаем множество компонент связности каждая из которых содержит ровно одну вершину.

3. Пока компонент связности больше чем одна.

   1. Взять ребро из начала списка ребер.

   2. Если ребро соединяет две разных компоненты связности то

      1. Компоненты связности объединить в одну.

 

Определение структур

struct REBRO{

int v1,v2,Cost;

};

struct GRAPH{

int nVersh; // число вершин графа

int nReber; // числ ребер графа

int *Versh; // номера компонент связности

REBRO *Rebro; // массив ребер

int nOstovReber; // число ребер в остове

REBRO *OstovRebro; // ребро, принадлежащее остовному дереву

};

Implementation

void KruskalOstov(GRAPH *gr){

// эту функцию НАПИШИТЕ САМИ

int i,j;

int v1,v2; // номера вершин ребра

int n1,n2; // номера компонент связности вершин v1,v2

int nr=0; // число ребер уже включенных в остовный граф

for(i=0; i<gr->nVersh; i++){

gr->Versh[i]=i;

}

qsort(gr->Rebro,gr->nReber,sizeof(REBRO),rcmp);

for(i=0;i<gr->nReber;i++){

v1=gr->Rebro[i].v1;

v2=gr->Rebro[i].v2;

n1=gr->Versh[v1];

n2=gr->Versh[v2];

if(n1==n2){ // вершины относятся к одной компоненте связности

continue;

}

// включаем ребро в остовное дерево

memcpy(gr->OstovRebro+nr++,gr->Rebro+i, sizeof(REBRO));

// все вершины с компонентой связности n2 относим к компоненте n1

for(j=0; j<gr->nVersh; j++){

if(gr->Versh[j]==n2){

gr->Versh[j]=n1;

}

}

}

gr->nOstovReber=nr;

}

Графы

Ориентированные и неориентированные графы – естественная модель отношений между какими-либо объектами.

Ориентированный граф (орграф) G=(V,E) состоит из множества вершин V и множества дуг E. Вершины также называют узлами, а дуги – ориентированными ребрами.

П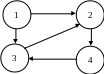 ример орграфа с 4 вершинами 5 ребрами.

Вершины орграфа можно использовать для представления объектов, а дуги для отношений между объектами. Например, вершины орграфа могут представлять города, а дуги – маршруты полетов самолетов из одного города в другой. Или, другой пример, вершины – блоки операторов программы, а дуги – перемещение потоков данных.

Путем в орграфе называется последовательность вершин v₁, v₂,…, v_n, для которой существуют дуги v₁ v₂, v₂ v₃,…, v_n-1  v_n. Длина пути – количество дуг, составляющих путь. Путь называется простым, если все вершины на нем, за исключением, может быть, первой и последней, различны. Цикл – это простой путь длины не менее 1, который начинается и заканчивается в одной и той же вершине. На рис. вершины 3,2,4,3 образуют цикл длины 3.

Во многих приложениях удобно к вершинам и дугам орграфа присоединить какую-либо информацию. Для этих целей используется помеченный орграф, т.е. орграф, у которого каждая дуга и/или каждая вершина имеет соответствующие метки. Меткой может быть имя, вес, стоимость (дуги), или значение данных какого-либо заданного типа.