Представление графа в программе.
Пусть дан смешанный граф:
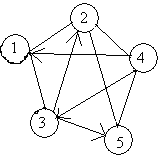
Рис. 6. Смешанный граф.
Известно несколько способов представлений графа G=(V, Е) в памяти компьютера.
Матрица смежности.
Матрица смежности - это матрица размером n×n, в которой cij=1, если существует ребро из i в j и cij=0 в противном случае.
Например для вышеприведенного графа матрица смежности будет иметь следующий вид:
|
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
1 |
0 |
0 |
2 |
1 |
0 |
0 |
1 |
1 |
3 |
1 |
1 |
0 |
0 |
1 |
4 |
1 |
1 |
1 |
0 |
1 |
5 |
0 |
1 |
0 |
1 |
0 |
Для неориентированного графа справедливо cij=cji и матрица смежности симметрична.
Представление в виде матрицы смежностей удобно для тех алгоритмов на графах, которым часто нужно знать, есть ли в графе данное ребро, ибо время, необходимое для определения наличия ребра, фиксировано.
В тех случаях, когда ребра имеют веса (например, роль веса играет расстояние между вершинами или стоимость перемещения из вершины в вершину), элементы матрицы смежности – веса рёбер. Признаком отсутствия ребра в этом случае является не 0, а ∞, что означает бесконечно большое расстояние или стоимость. В качестве значения ∞ в программе можно использовать FLT_MAX для величин типа float и DBL_MAX для double, определённые в float.h.
Данные, хранимые в матрице смежности, могут быть представлены также массивом структур, содержащим списки смежности, вида:
struct VERSHINA {
int nr; // число вершин, смежных с данных
int *sm; // массив номеров вершин, смежных с данной
};
Массив можно заменить линейным списком.
Полное описание графа для случая, когда вершины и ребра обладают дополнительными свойствами, может быть представлено, например, следующими структурами:
struct REBRO{
int w; // номер смежной вершины
<свойства ребра>;
};
struct VERSHINA{
<свойства вершины>;
int nr; // число вершин, смежных данной (число ребер)
REBRO *Rebro; // массив рёбер
};
struct GRAPH{
int nv; // число вершин
VERSHINA *v; // массив вершин
};
Массивы могут быть заменены на списки.
Матрица инцидентности
Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность).
В случае ориентированного графа каждому ребру <x,y> ставится в соответствие "-1" на позиции (x,y) и "1" на позиции (y,x); если связи между вершинами нет, то ставится в соответствие "0".
Пример
-
Граф
Матрица инцидентности
В каждом столбце должны стоять две единицы, а все остальные символы - нули.
Массив ребер.
Массив ребер – это массив, в котором ребра хранятся парами вершин, которые они соединяют.
Это наиболее понятный, но достаточно неудобный способ хранения графа. Однако у него есть один большой плюс - при таком способе представления легко вводить дополнительные характеристики ребер. Для этих целей в структуру, содержащую описание ребра могут быть добавлены дополнительные элементы, например:
struct REBRO{
int v,w; // вершины
float Weight; // вес ребра
};
Для представления конечного автомата структура могла бы иметь вид:
struct REBRO{
int v,w; // состояния автомата
int Symbol; // входной символ
void (*f)(); // функция, выполняемая на переходе
};
Для не ориентированного графа можно при наличии описания ребра (v,w) не включать описание (w,v);