Составитель

Гайворонская С. А.

Линейная алгебра

курс лекций

Воронеж

2012

УДК 004.4

ББК 32.973

Утверждено научно-методическим советом факультета международных отношений ВГУ от 19.09.2012г., протокол №7.

Рецензент:

заведующий кафедрой высшей математики и физико-математического моделирования Воронежского государственного технического университета, доктор физико-математических наук, профессор И.Л. Батаронов

Гайворонская С. А. Линейная алгебра : курс лекций для студентов факультета международных отношений / С. А. Гайворонская. – Воронеж : ФМО ВГУ, 2012. – 91 с.

Пособие подготовлено на кафедре международной экономики и внешнеэкономической деятельности факультета международных отношений Воронежского государственного университета.

Учебное пособие предназначено для студентов, обучающихся на факультете международных отношений по направлению «Экономика», «Международные отношения», «Регионоведение».

В пособии излагаются все изучаемые темы, предусмотренные программой. Приводится теоретический материал, большое количество примеров решения задач по рассмотренным темам.

Тема 1. Матрицы. Определители.

1.1. Матрицы.

Определение. Прямоугольная таблица чисел вида

называется матрицей,

где - действительные числа, называемые элементами матрицы, ; , и - соответственно индексы строки и столбца.

Произведение числа строк на число столбцов называют размером матрицы.

Матрицы обозначаются прописными латинскими буквами А, В.

Часто матрицу записывают в сокращенном виде .

С помощью матриц удобно записывать некоторые экономические зависимости, например, таблицу распределения ресурсов, усл.ед., по отдельным отраслям экономики

Ресурсы	Отрасль экономики
	Промышленность	Сельское хозяйство
Энергетические	5,3	4,1
Трудовые	2,8	2,1
Водные	4,8	5,1

может быть записана в компактной форме в виде матрицы

В этой записи матричный элемент показывает, сколько электроэнергии потребляет промышленность, а элемент - сколько водных ресурсов требуется для сельского хозяйства.

Виды матриц

Матрица, состоящая из одной строки, называется матрицей-строкой или вектором-строкой: .

Матрица, состоящая из одного столбца, называется матрицей-столбцом или вектором-столбцом: .

Если число строк матрицы n-го порядка равно числу ее столбцов, т.е. , то матрица называется квадратной n-го порядка.

Например: 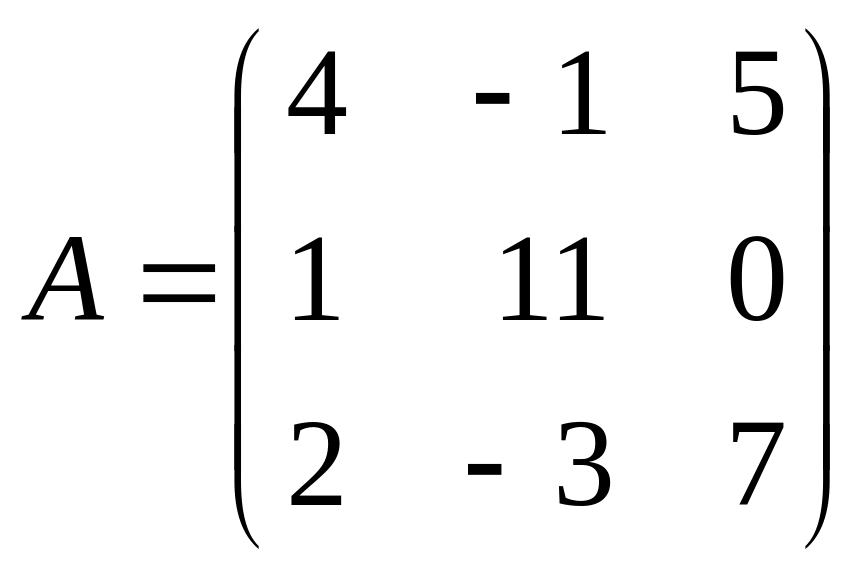- квадратная матрица, размером .

Упорядоченная совокупность элементов называется главной диагональю квадратной матрицы:

Квадратная матрица называется диагональной, если ненулевыми могут быть только элементы главной диагонали, т.е. матрица имеет вид:

.

Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны единице:

- единичная матрица третьего порядка.

Матрица, все элементы которой равны нулю, называется нулевой матрицей.

Две матрицы и называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны.

Симметрические матрицы - это квадратные матрицы, у которых элементы симметричные относительно главной диагонали равны, т.е. , , .

Например: , , , .

2. Операции над матрицами.

1. Умножение матрицы на число

Произведением матрицы А на действительное число называется матрица, каждый элемент которой равен произведению соответствующего элемента матрицы А на число .

Пример.

;

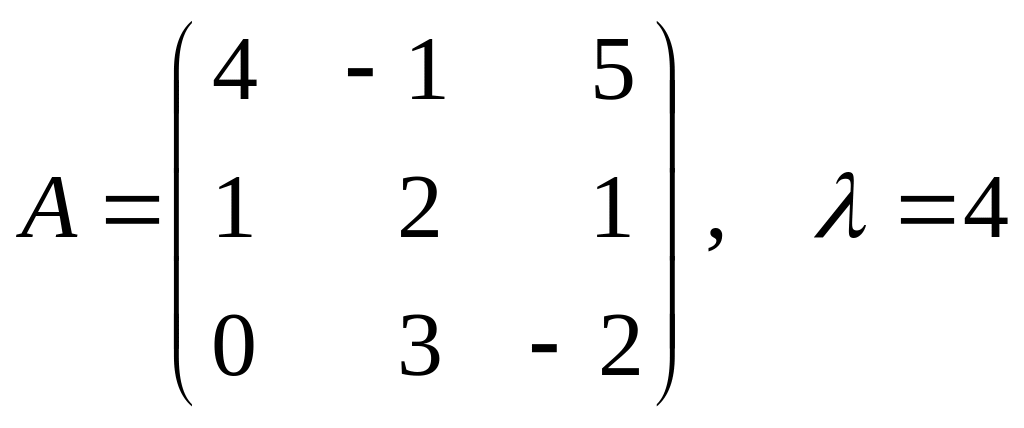Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы, например:

2. Сложение матриц

Суммой двух матриц и одинакового размера называется матрица каждый элемент которой равен сумме соответствующих элементов матриц и : , т.е. матрицы складываются поэлементно.

Пример.

Свойства операций суммирования матриц и произведения матрицы на число, непосредственно вытекающие из определений этих операций.

Пусть , и – матрицы, имеющие одинаковый размер, а и – некоторые действительные числа, тогда:

1. .

2. .

3. .

4. .

5. .

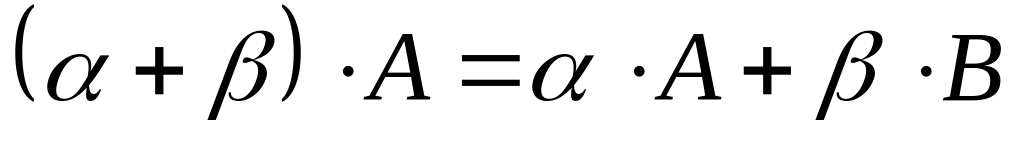6. , где - нулевая матрица.

7. .