
- •А.А.Светашков, к.Н.Цукублина сопротивление материалов
- •Оглавление
- •Лекция 1. Введение
- •1.1 Наука о сопротивлении материалов
- •1.2 Модель объекта исследования
- •1.3 Схематизация геометрии объекта расчёта (модели формы)
- •1.4 Допущения о характере деформации
- •1.5 Классификация внешних сил
- •1.6 Внутренние усилия. Виды нагружений
- •1.7 Напряжения
- •1.8 Перемещения и деформации
- •Лекция 2. Растяжение, сжатие
- •2.1 Определение внутренних усилий
- •2.2 Напряжение в поперечном сечении растянутого стержня
- •2.3 Деформации и перемещения при растяжении, сжатии
- •2.4 Связь между напряжением и деформацией
- •2.5 Учёт влияния собственного веса
- •2.6 Расчёт статически неопределимых систем
- •2.7. Испытание на растяжение. Определение характеристик прочности
- •2.8 Определение допускаемых напряжений
- •2.9 Определение характеристик пластичности
- •Лекция3. Сдвиг, срез, смятие
- •3.1 Напряжения и деформации
- •3.2 Практические расчеты на срез и смятие
- •Лекция 4. Геометрические характеристики плоских сечений
- •4.1 Виды геометрических характеристик
- •4.2 Общие свойства геометрических характеристик
- •4.3 Моменты инерции простейших геометрических фигур
- •4.4 Моменты сопротивления
- •Моменты сопротивления простейших сечений
- •4.5 Зависимость между моментами инерции относительно параллельных осей, одна их которых центральная
- •4.6 Главные оси и главные моменты инерции сечения
- •Лекция 5. Кручение
- •5.1 Распределение касательных напряжений при кручении
- •5.2 Связь между касательным напряжением и внутренним крутящим моментом
- •5.3 Условие прочности при кручении
- •5.4 Построение эпюр угловых перемещений при кручении
- •5.5 Условие жесткости при кручении
- •Лекция 6. Изгиб
- •6.1 Классификация нагрузок, производящих изгиб
- •6.2 Понятие об изгибающем моменте и перерезывающей силе
- •6.3 Правило знаков для q, m
- •6.4 Зависимость между изгибающим моментом, поперечной силой и интенсивностью погонной нагрузки (теоремы Журавского)
- •6.5 Нормальные напряжения при чистом изгибе
- •6.6 Связь между нормальным напряжением и изгибающим моментом
- •6.7 Условие прочности при изгибе
- •6.8 Определение касательных напряжений
- •6.9 Деформации и перемещения при изгибе
- •6.10 Метод начальных параметров
- •6.11 Условие жесткости при изгибе
- •Лекция 7. Теория напряженного состояния
- •7.1 Исследование напряженного состояния при растяжении
- •7.2 Плоское напряженное состояние
- •7.3 Деформации при объемном напряженном состоянии. Обобщенный закон Гука
- •7.4 Потенциальная энергия упругой деформации
- •7.5 Проверка прочности в общем случае сложного напряженного состояния. Теории прочности
- •Лекция 8. Действие динамических нагрузок
- •8.1 Равноускоренное движение
- •8.2 Определение перемещений и напряжений при ударе
- •8.3 Колебания упругих систем
- •8.4 Собственные колебания без затухания
- •8.5 Собственные колебания с затуханием
- •8.6 Вынужденные колебания. Резонанс
- •Лекция 9. Продольный изгиб (устойчивость сжатых стержней)
- •9.1 Задача Эйлера определения критической силы
- •9.2 Влияние способов закрепления стержня
- •9.3 Предел применимости формулы Эйлера
- •9.4 Практическая формула расчета на устойчивость
- •9.5 Рациональные формы сечений
- •Сопротивление материалов
7.2 Плоское напряженное состояние
Анализируя плоское напряженное состояние, установим связь между главными напряжениями и напряжениями, действующими на наклонных площадках (рис. 7.4, а).
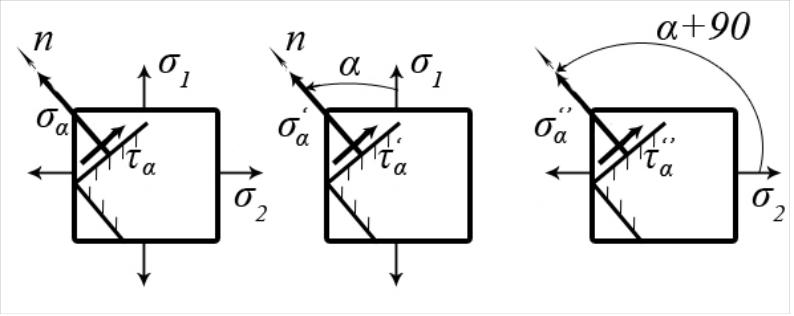
а) б) в)
Рис.7.4
Поскольку здесь два отличных от нуля напряжения, условимся отсчитывать угол наклона площадки от большего из двух напряжений (рис.7.4,б).
Применяя принцип суперпозиции, будем рассматривать данное напряженное состояние как наложение двух ортогональных одноосных напряженных состояний (рис 7.4, б, 7.4, в). В соответствии с принятым:
![]() . (7.5)
. (7.5)
При вычислении напряжений воспользуемся
непосредственно формулами (7.3) и (7.4).
Нормаль n составляет
с направлением
![]() угол
,
с направлением
угол
,
с направлением
![]() – угол
– угол
![]() .
Вычисляя, получим:
.
Вычисляя, получим:
![]() (7.6)
(7.6)
![]() (7.7)
(7.7)
Определим напряжения на площадке
![]() ,
перпендикулярной к площадке
,
перпендикулярной к площадке
![]() ; (7.8)
; (7.8)
![]() . (7.9)
. (7.9)
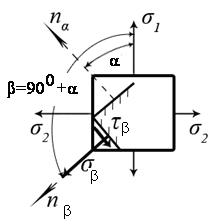
Рис.7.5
Сравнивая формулы (7.7) и (7.9),замечаем,
что
![]() .
Касательные напряжения на взаимно
перпендикулярных площадках равны по
величине и противоположны по знаку, что
выражает закон парности касательных
напряжений.
.
Касательные напряжения на взаимно
перпендикулярных площадках равны по
величине и противоположны по знаку, что
выражает закон парности касательных
напряжений.
Условимся считать касательное напряжение положительным, если оно стремится повернуть элемент по часовой стрелке.
Нормальные напряжения положительны, если они совпадают по направлению с положительной нормалью к грани элемента.
Суммируя левые и правые части уравнений (7.6) и (7.8), обнаруживаем, что
![]() ,
,
т.е. сумма нормальных напряжений на взаимно перпендикулярных площадках есть величина постоянная.
Проведя соответствующие исследования,
замечаем, что касательные напряжения
достигают экстремального значения на
площадках расположенных под углом
![]() к главным.
к главным.
Нормальные напряжения экстремальны на главных площадках.
Таким образом, для практических расчетов более важной задачей является определение главных напряжений.
В том случае, когда известны нормальные и касательные напряжения, действующие на двух взаимно перпендикулярных площадках, аналитические выражения для определения главных напряжений имеют вид:
![]() ; (7.10)
; (7.10)
![]() . (7.11)
. (7.11)
Если одно из вычисленных главных
напряжений окажется положительным, а
другое отрицательным их следует
обозначать
и
![]() соответственно. Если отрицательны оба
главных напряжения, то меньшее по модулю
напряжение следует обозначить
,
а большее
.
соответственно. Если отрицательны оба
главных напряжения, то меньшее по модулю
напряжение следует обозначить
,
а большее
.
Величины главных напряжений и положение главных площадок можно определить и графически, построив для этого, так называемый , круг напряжений, или круг Мора.
Построение круга напряжений ведут в
системе отсчета
![]() и
и
![]() .
.

Рис 7.6
Ось – направлена по горизонтали, – по вертикали.
Каждая точка круга напряжений представляет одну из площадок, характеризуемых определенными значениями и .
Строим точку D круга, откладывая
 и
и
 в соответствии с оговоренными ранее
правилами знаков. Точка D
соответствует площадке
.
Точка
в соответствии с оговоренными ранее
правилами знаков. Точка D
соответствует площадке
.
Точка
 с координатами
с координатами
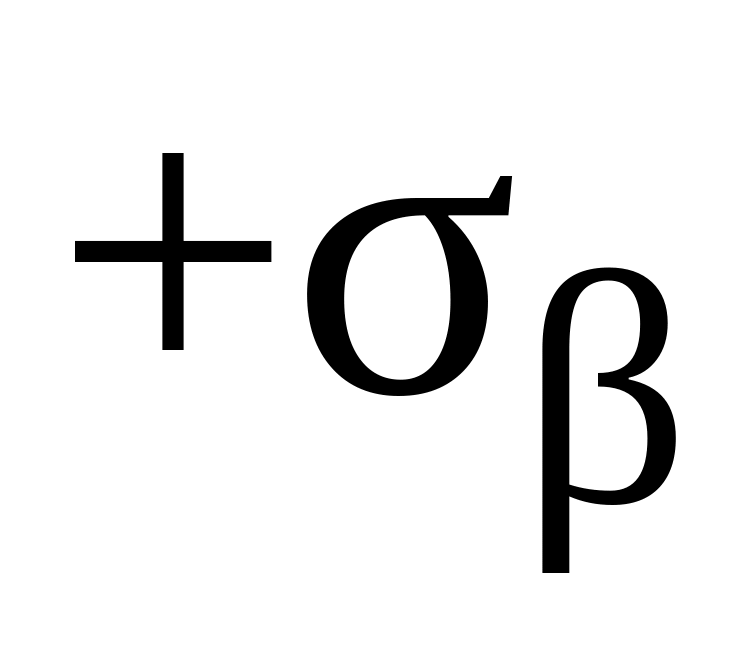 ,
,
 представляет площадку
.
представляет площадку
.Соединяем точки D и прямой. В пересечении с горизонтальной осью получается центр круга напряжений C.
Радиусом CD=C проводим окружность
Точки A и B представляют главные площадки, т.к. координаты этих точек равны нулю, а

Отрезки OB и OA могут быть представлены в виде OB=OC+CB, OA=OC-CA. Поскольку радиусы круга CB=CD, СA=CD, можно записать
![]() , (7.12)
, (7.12)
![]() . (7.13)
. (7.13)
Как легко увидеть OC=OK+KC,
где
![]() .
.
Подставляя полученное в (7.12) и (7.13) запишем
 ,
(7.14)
,
(7.14)
ч
Рис. 7.7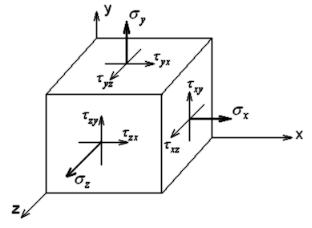
шесть остальных – касательные напряжения с двумя индексами: первый соответствует нормали к площадке, второй – направлению оси параллельной рассматриваемому τ. Эта совокупность напряжений называется тензором напряжений. Изменяя направление секущих плоскостей можно выйти на главные площадки, где касательные напряжения равны нулю, а нормальные достигают экстремальных значений
Определение положения главных площадок и направления действия главных напряжений позволяет профессионально создавать железобетонные конструкции. Именно в направлении действия главных напряжений укладывают металлические стержни в железобетонной балке, повышая ее прочность и жесткость.
