
- •1. История разв метрологии. Осн пон, термины, опред.
- •2. Основные понятия
- •4. Шкала измерений
- •5. Виды физических величин
- •6. Системы единиц физических величин.
- •7. Общая классифик-я погр-ей измер-й.
- •7. Погрешности измерений(в лекции короче)
- •10. Аддтитивные и мультипликативные погрешности
- •12. Законы распределения случайных погрешностей(в лекциях лучше вроде)
- •13.Грубые промахи и их оценка
- •14. Оценка точности прямых многократных равноточных измер-й.
- •15.Оценка погр-ти техн-их измер-ий по их классу точности.
- •16. Оценка точности прямых многокр-х неравнот-ых измер-ий.
- •22. Номенклатура нормируемых метрологически характеристик
- •24. Субъекты и нормативная база метрологии.
- •25. Поверка и калибровка средств изм-й. Поверочные схемы.
- •26. Основные понятия и определения ст-и.
- •27. Цели, принципы и функции стандартизации.
- •28 Методы стандартизации
- •32 Порядок разработки нац. Ст-тов.
- •35. Техн-ие усл-ия как нормативный док-т
- •37 Международная и региональная стандартизация.
- •39Осн цели и принципы сертиф
- •41.Субъекты обязательной сертификации
- •42. Субъекты добровольной сертификации
- •43 Правила и норматив база серт.
- •44. Формы обязательного и добровольного подтверждения соответствия
- •4. Обязательное подтверждение соответствия
- •45.Схемы сертификации
- •46. Порядок провед-я сертификации.
- •47. Порядок серт-ии пр-ии, ввозимой из-за рубежа.
- •48. Особ-ти сертиф-ции продоволь-х товаров
- •49. Сертиф-ция непродов-х товаров
- •50. Сертиф-ция работ и услуг
14. Оценка точности прямых многократных равноточных измер-й.
Многокр-е изм-я –
не менее 4 значений измер-й вел. Получаем
ряд х1,х2,…Хn
. Причем
каждый результат измерений может
содержать как систематическую, так и
случайную погр-ть, тогда в общем случае
каждый Хi
= Хист.
+ Δист
+ Δслуч.
После исключения известных систематич-х
погр-ей каждый рез-т может выч-ся как Х1
= Хист+
Δслуч
+ Δнс
(неискл-е систем-е погр-ти). Дальн-я
обработка рез-в м.б. представлена в виде
последовательности или алгоритма,
направленного на нахождение погр-ти
при усл-и известного закона распределения
. Мх
=
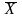 ; σ = S.
; σ = S.
В России есть ст-т ГОСТ 8.207 – 76. Прямые измер-я с многократными наблюдениями. Методы обр-ки рез-в наблюдений.
Задача. Опр-ть рез-т многокр-х измер-й (n=5) размера Х детали с пом-ю вертик-го длинномера ИЗВ – 1, имеющего неисключ-ю систематич-ю погр-ть с границами θ =± (1,2 + Х/120). Р дов = 0,95. Рез-ты: 36,5340; 36,5316; 36,5325; 36,5341; 36,5338.
1)Искл-е известных систем-х погр-ей из рез-в. Пол-е исправл-х рез-в изм-й. Хi = Х’i - Δсист.Хi. Для условий примера ноличие сист-й погр-ти не оговорено.
2)Вычисление среднего арифметического исправл-х рез-в наблюдений. Оно принимается за рез-т измер-й. =36,5332 мм.
3)Вычисление
оценки среднего квадратического
отклонения рез-та набл-я.
 Для наших усл-й эта величина =0,0011
мм = 1,1 мкм
Для наших усл-й эта величина =0,0011
мм = 1,1 мкм
4) Выявление
возможных грубых промахов.
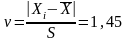 < νд
(5; 0,95) = 1,84 Вывод: данный рез-т не сод-т
грубой погр-ти и д.б. оставлен для дальн-ей
обработки. В случае выявления грубого
промаха он искл-ся из обрабатываемых
данных и пункты 2) и 3) необходимо повторить.
< νд
(5; 0,95) = 1,84 Вывод: данный рез-т не сод-т
грубой погр-ти и д.б. оставлен для дальн-ей
обработки. В случае выявления грубого
промаха он искл-ся из обрабатываемых
данных и пункты 2) и 3) необходимо повторить.
5) Вычисление оценки
среднего кв-го откл-я рез-та изм-й.
 , где n
– кол-во отдел-х рез-в.
, где n
– кол-во отдел-х рез-в.
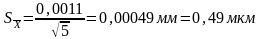
По сути
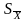 является значением случайной погр-ти
рез-та изм-й. Но как показывает практика,
этого недостаточно.
является значением случайной погр-ти
рез-та изм-й. Но как показывает практика,
этого недостаточно.
6) Вычисление
доверительных границ случ-й погр-ти
рез-та изм-й. Критерий Стьюдента Е = ±
t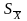 ,
где t
– коэффициент Стьюдента, зависящий от
доверительной вер-ти и числа степеней
свободы (n-1).
Определяется по статистическим таблицам.
t0,95;4
= 2,78, тогда Е = +-1,36 мкм. Замечание: в
некоторых случаях бывает необходимо
доказать принадлежность обраб-ха рез-в
к нормальному или другому распределению.
,
где t
– коэффициент Стьюдента, зависящий от
доверительной вер-ти и числа степеней
свободы (n-1).
Определяется по статистическим таблицам.
t0,95;4
= 2,78, тогда Е = +-1,36 мкм. Замечание: в
некоторых случаях бывает необходимо
доказать принадлежность обраб-ха рез-в
к нормальному или другому распределению.
7) Вычисление границ
неисключенной систематической погрешности
рез-в изм-й. при числе составляющих m
меньше либо равно 3 общие границы
вычисляются
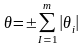 .
m>3,
.
m>3,
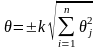 .
k
– коэф-т, зависящий от Рдов и числа
составляющих m.
Для нашего примера
.
k
– коэф-т, зависящий от Рдов и числа
составляющих m.
Для нашего примера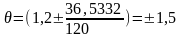 мкм.
мкм.
=± 0,49, Е = ±1,36 мкм, θ=± 1,5 мкм – граница неисключенной составляющей.
8) Нахождение доверительных границ полной погрешности. 0,8 < … < 8. Если значение меньше 0,8, то учитывается , если больше 8, то … , если между 0,8 … 8, то учитываем обе составляющие. 1,5/0,49=3 – необходимо учитывать обе составляющие.
9) Расчет общей
погрешности.
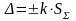 ,
,
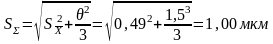 ,
,
Δ = 2,1*1 = 2,1 мкм =0,0021мм
10) Запись окончательного результата измерений и погрешности. = (36,5332±0,0021) мм, Рдов = 0,95, n=5
