3. Основные понятия теории вероятностей.

• Событием называется любой исход опыта, различают следующие виды событий:

- случайные

- достоверные

- невозможные

Понятие достоверного и невозможного события используется для

количественной оценки возможности появления того или иного явления, а с

количественной оценкой связана вероятность.

• Вероятность — численная мера возможности наступления некоторого события.

• Вероятностное пространство

• Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

4. Вероятностное пространство.

Вероя́тностное простра́нство — понятие, введённое А. Н. Колмогоровым в 30-х годах XX века для формализации понятия вероятности, которое дало начало бурному развитию теории вероятностей как строгой математической дисциплины.

Вероятностное пространство — это тройка   (иногда обрамляемая угловыми скобками:  ), где

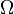•  — это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;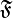

•  — сигма-алгебра подмножеств  , называемых (случайными) событиями;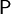

•  — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что  .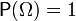

Замечания

• Элементарные события (элементы  ), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.

• Каждое случайное событие (элемент  ) — это подмножество  . Говорят, что в результате эксперимента произошло случайное событие 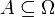 , если (элементарный) исход эксперимента является элементом 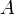 . Требование, что   является сигма-алгеброй подмножеств  , позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.

Простым и часто используемым примером вероятностного пространства является конечное пространство. Пусть   — конечное множество, содержащее   элементов.

В качестве сигма-алгебры удобно взять семейство подмножеств  . Его часто символически обозначают  . Легко показать, что общее число членов этого семейства, т.е. число различных случайных событий, как раз равно  , что объясняет обозначение.

Вероятность, вообще говоря, можно определять произвольно. Часто, однако, нет причин считать, что один элементарный исход чем-либо предпочтительнее другого. Тогда естественным способом ввести вероятность является:

,

где  , и   - число элементарных исходов, принадлежащих  .

В частности, вероятность любого элементарного события:

5. Непосредственный подсчет вероятности.

Основные правила комбинаторики. Правило умножения (основная теорема комбинаторики). Общее число N способов, которыми можно получить упорядоченную совокупность (a₁,a₂,...a_k), где a_iA_i (т.е. выбрать по одному элементу из каждой группы и расставить их в определенном порядке), равно

.

Б. Правило сложения. Если один элемент из группы A_i можно выбрать n_i способами, и при этом любые две группы A_i и A_j не имеют обших элементов, то выбор одного элемента или из A₁, или из A₂, ..., или из A_k можно осуществить

способами.

размещения – это упорядоченные совокупности k элементов из n, отличающиеся друг от друга либо составом, либо порядком элементов.

Например. Пусть имеется множество из трех элементов. Тогда все размещения двух элементов из трех таковы:

Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов.

Число всех перестановок множества из n элементов обозначается и вычисляется по формуле

.

сочетания – это неупорядоченные совокупности элементов, отличающиеся друг от друга только составом элементов.

Например. Все сочетания без повторений двух элементов из множества :

Формула для вычисления числа сочетаний n элементов по k: