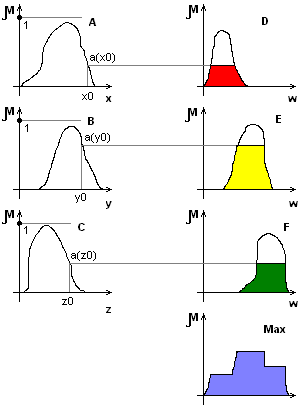П риведение к чёткости. Основной метод – центроидный метод.

Пример

П1: Если x есть A, то w есть D

П2: Если y есть B, то w есть E

П3: Если z есть C, то w есть F

где x, y, z – имена входных переменных,

w – имя переменной вывода,

A, B, C, D, E, F – заданные ф-ции принадлежности

Этапы вывода

1. Нахождение a(x0), a(y0), a(z0).

2. Отсекание функций принадлежности D, E, F по a(x0), a(y0), a(z0) соответственно.

3. Объединение ф-ций принадлежности по Max.

4. При необходимости находим чёткое значение выходной переменной (центроидны метод).

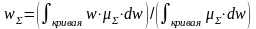
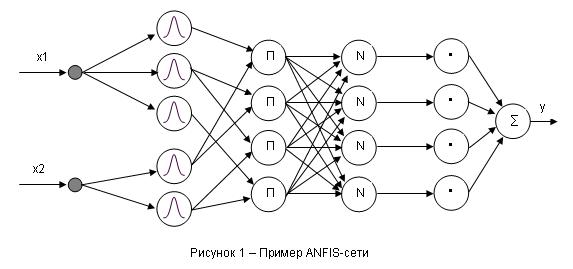
2.ANFIS

ANFIS - это аббревиатура Adaptive-Network-Based Fuzzy Inference System - адаптивная сеть нечеткого вывода. Она была предложена Янгом (Jang) в начале девяностых. ANFIS является одним из первых вариантов гибридных нейро-нечетких сетей - нейронной сети прямого распространения сигнала особого типа. Архитектура нейро-нечеткой сети изоморфна нечеткой базе знаний. В нейро-нечетких сетях используются дифференцируемые реализации треугольных норм (умножение и вероятностное ИЛИ), а также гладкие функции принадлежности. Это позволяет применять для настройки нейро-нечетких сетей быстрые алгоритмы обучения нейронных сетей, основанные на методе обратного распространения ошибки. Ниже описываются архитектура и правила функционирования каждого слоя ANFIS-сети.

ANFIS реализует систему нечеткого вывода Суджено в виде пятислойной нейронной сети прямого распространения сигнала. Назначение слоев следующее:

первый слой - термы входных переменных;

второй слой - антецеденты (посылки) нечетких правил;

третий слой - нормализация степеней выполнения правил;

четвертый слой - заключения правил;

пятый слой - агрегирование результата, полученного по различным правилам.

Входы сети в отдельный слой не выделяются. На рис. 1 изображена ANFIS-сеть с двумя входными переменными (x1 и x2) и четырьмя нечеткими правилами. Для лингвистической оценки входной переменной x1 используется 3 терма, для переменной x2 - 2 терма.

Введем следующие обозначения, необходимые для дальнейшего изложения:

x1, x2, …, xn - входы сети;

y - выход сети;

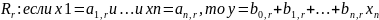- нечеткое правило с порядковым номером r;

m - количество правил r = [1..m];

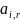- нечеткий терм с функцией принадлежности 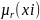, применяемый для лингвистической оценки переменной в r-ом правиле (r = [1..m], i = [1..n]);

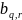- действительные числа в заключении r-го правила (r = [1..m], q = [0..n]).

ANFIS-сеть функционирует следующим образом.

Слой 1. Каждый узел первого слоя представляет один терм с колокообразной функцией принадлежности. Входы сети x1, x2,…,xn соединены только со своими термами. Количество узлов первого слоя равно сумме мощностей терм-множеств входных переменных. Выходом узла являются степень принадлежности значения входной переменной соответствующему нечеткому терму:

,

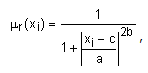где a, b и c - настраиваемые параметры функции принадлежности.

Слой 2. Количество узлов второго слоя равно m. Каждый узел этого слоя соответствует одному нечеткому правилу. Узел второго слоя соединен с теми узлами первого слоя, которые формируют антецеденты соответствующего правила. Следовательно, каждый узел второго слоя может принимать от 1 до n входных сигналов. Выходом узла является степень выполнения правила, которая рассчитывается как произведение входных сигналов. Обозначим выходы узлов этого слоя через , .

Слой 3. Количество узлов третьего слоя также равно m. Каждый узел этого слоя рассчитывает относительную степень выполнения нечеткого правила:

.

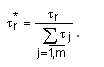Слой 4. Количество узлов четвертого слоя также равно m. Каждый узел соединен с одним узлом третьего слоя а также со всеми входами сети (на рис. 1 связи с входами не показаны). Узел четвертого слоя рассчитывает вклад одного нечеткого правила в выход сети:

.

Слой 5. Единственный узел этого слоя суммирует вклады всех правил:

.

Типовые процедуры обучения нейронных сетей могут быть применены для настройки ANFIS-сети так как, в ней использует только дифференцируемые функции. Обычно применяется комбинация градиентного спуска в виде алгоритма обратного распространения ошибки и метода наименьших квадратов. Алгоритм обратного распространения ошибки настраивает параметры антецедентов правил, т.е. функций принадлежности. Методом наименьших квадратов оцениваются коэффициенты заключений правил, так как они линейно связаны с выходом сети. Каждая итерация процедуры настройки выполняется в два этапа. На первом этапе на входы подается обучающая выборка, и по невязке между желаемым и действительным поведением сети итерационным методом наименьших квадратов находятся оптимальные параметры узлов четвертого слоя. На втором этапе остаточная невязка передается с выхода сети на входы, и методом обратного распространения ошибки модифицируются параметры узлов первого слоя. При этом найденные на первом этапе коэффициенты заключений правил не изменяются. Итерационная процедура настройки продолжается пока невязка превышает заранее установленное значение. Для настройки функций принадлежностей кроме метода обратного распространения ошибки могут использоваться и другие алгоритмы оптимизации, например, метод Левенберга-Марквардта.

3. Представление знаний в эс: логическое, продукционное, фреймовое. Достоинства и недостатки

Представление определяется как "множество синтаксических и семантических соглашений, которое делает возможным описание предмета". В ИИ под "предметом" понимается состояние в некоторой проблемной области, например объекты в этой области, их свойства, отношения, которые существуют между объектами. Описание позволяет использовать соглашения из представления для описания определенных предметов.

Для представления знаний используются следующие модели:

1. Логические – базируются на представлении знаний в системе логики предикатов первого порядка. Правила формальной логики постепенно расширяются, приближаясь к человеческой, которая характеризуется нечеткостью. В связи с чем появились модальная, многозначная, немонотонная, псевдофизическая и другие виды логик.

2. Продукционные – представляют знания в форме предикатов первого порядка, а правила манипулирования ими – с помощью конструкций ЕСЛИ – ТО. База знаний состоит из множества правил типа: «ЕСЛИ рентабельность снизилась И прибыль увеличилась ТО себестоимость продукции выросла».

3. Фреймовые – отражают систематизированную в виде единой теории модель памяти человека. Основной элемент модели – фрейм – отражает структуру данных для описания понятийных структур классов, объектов. Все фреймы взаимосвязаны и образуют единую систему, в которой объединены факты (описательные знания), правила (содержащие И, ИЛИ) и процедуры их обработки. С помощью фреймов можно определить объекты с наследуемыми свойствами и конструкции структуры более общего характера с большим числом возможностей.

4. Семантическая сеть – структура данных, несущая определенный смысл в виде целостного образа сети, узлы которой соответствуют понятиям и объектам, а дуги – отношением между объектами.

5. Нейро-нечеткие модели.

Логическая модель

Правила, факты и цели задаются следующим образом (с помощью грамматики Бэкуса-Наура):

<правило> ::= <заголовок правила> > <список условий>

<список условий> ::= <условие> | <список условий> & <условие>

<условие> ::= <предикат> ( <список термов> )

<список термов> ::= <терм> | <список термов>, <терм>

<терм> ::= <константа> | <переменная>

<факт> ::= <предикат> (<список констант>)

<список констант> ::= <константа> | <список констант>,<константа>

<цель> ::= <предикат> (<список констант>)

Правила вывода обеспечивают создание новых предложений на основае данных предложений и фактов. Для применения правила вывода система вывода должна уметь определять, когда выражения являются эквивалентными. Определение равносильности осложнено наличием переменных. Переменная может быть заменена любым термом (в т.ч. переменной).

Унификация – алгоритм определения необходимых подстановок с целью приведения в соответствие двух выражений исчисления предикатов.

Продукционная модель

Правила задаются следующим образом (условие и заключение) (с помощью грамматики Бэкуса-Наура):

<правило> ::= (ЕСЛИ {<антецедент>} ТО {<консеквент>} )

<антецедент> ::= <ассоциативная тройка>

<консеквент> ::= <ассоциативная тройка>

<ассоциативная тройка> ::= (<атрибут><объект><значение>)

<атрибут>, <объект> и <значение> должны быть специальными терминами предметной области.

Семантическая сеть

Вершины в семантической сети – понятия, свойства, события.

понятия – сведение об абстрактных или физических объектах предметной области.

события – действия в реальном мире.

свойства – уточнение понятий.

Дуги сети (семантические отношения) делят на четыре класса:

• лингвистические (падежные, глагольные, атрибутивные). Отображает смысловую взаимосвязь между событиями, понятиями или свойствами.

• логические (И, ИЛИ, НЕ).

• теоретико-множественные (множество — подмножество, отношения целого и части, родовидовые отношения);

• квантифицированные (определяемые кванторами общности и существования).

Фреймы

Фрейм задается именем и слотом, которые могут заполняться конкретными значениями. Содержательная интерпретация слотов может быть различной. Это свойство в широком смысле слова: признаки, характеристики, бинарные отношения, роли, компоненты, атрибуты, валентность, аргументы и т.п. (одной из характеристик слота является тип значения, оно может быть задано ссылкой на другой фрейм так, что слоты служат в частности для описания отношений между фреймами (содержательно между понятиями)).

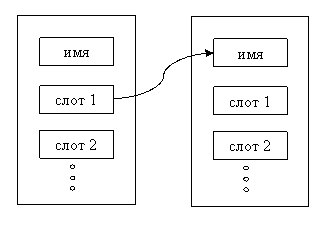
Особенности такого представления:

• знание организовано в виде совокупности взаимосвязанных описаний – классов данной предметной области;

• формальная структура для такого описания названа фреймом. Это дает возможность упаковать знания в подходящем образом организованные структуры, сохраняя его обозримость на всех уровнях;

• фреймы организуются в иерархии по уровню абстракции; конкретным объектам соответствуют экземпляры фреймов; свойства более общих понятий наследуются более конкретным в иерархии. Наследование представляет собой особый вид дедукции что дает выигрыш в эффективности и, что важнее, облегчает построение системы фреймов – базы знаний. Такие описания выглядят гораздо более близким к мыслительным структурам человека, нежели формализмы типа исчисления предикатов;

• структурное описание в виде содержаний ссылки на другие фреймы, что позволяет описывать различные отношения между понятиями данной предметной области; указанные ссылки могут иметь вид фрейма – прототипа с значениями его свойств-слотов. Сопоставление с прототипом также является механизмом, частично заменяющим обычную дедукцию, и, в то же время, более адекватным механизму мышления человека;

• с фреймами связываются процедуры, описывающие те или иные специализированные для данной предметной области процессы (проблемно-логический подход, поддержка целостности базы знаний, учет взаимосвязей экземпляров различных понятий и т.п.) Таким образом, фрейм представляет собой декларативно-процедурный модуль, включающий собственно предметную область, а также дополнительную информацию о способе его интерпретации.

Использование фреймов и их сетей наиболее полно удовлетворяет четырем основным требованиям к представлению знаний: внутренней интерпретируемости, структурируемости, связности и активности.

Следует отметить, что в настоящее время для реализации логического вывода во фреймо-ориентированных системах чаще всего используются прямые и обратные системы дедукции, основанные на правилах. Они не всегда оказываются эффективными по сравнению с методом резолюций, но действие таких систем легче воспринимается экспертами. Создание методов эффективного логического вывода в системах, основанных на фреймовом представлении, на практике оказывается труднореализуемой задачей.

Билет №3

Семантическая сеть – ориентированный граф с помеченными дугами и вершинами.

Вершины СС – понятия, события, свойства.

Понятия: сведения об абстрактных или физических объектах предметной области.

События: действие, происходящее в реальном мире, определяется указанием типа действия или ролей, которые играет объект.

Свойства: используются для уточнения понятий (особенности и характеристики) и событий (продолжительность, время, место).

Дуги СС отображают многообразие семантических отношений:

1. Лингвистические.

Смысловая взаимосвязь между событиями или понятиями или свойствами (глагольная, атрибутная, падежная).

2. Логические.

Операции алгебры логики.

3. Теоретико-множественные.

Отношения подмножеств, частей целого, множества и элемента.

4. Квантифицированные.

Логические кванторы общности и существования.

Пример.

Возьмем представление структуры понятий с помощью семантической сети.

В иерархической структуре понятий существует отношения, по крайней мере двух типов:

1. Отношение включения или совпадения (IS-A)

2. Отношение “целого-частного” (PART-OF).

Семантическая сеть, отображающая связи понятий при описании знаний о структуре понятия “юридическое лицо”. На рис. отображена структура понятий.

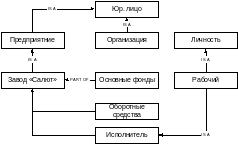
При представлении событий предварительно выделяются простые отношения, которые характеризуют основные компоненты событий:

1. В первую очередь из событий выделяется действие, которое обычно описывается глаголом.

2. Определяются объекты: которые совершают действия, над которыми действие совершается.

3. Все связи понятий, событий и свойств с действием навзывают падежами / падежными отношениями (лингвистическое отношение).

Получение вывода с помощью сс

Особенность семантической сети как модели знаний состоит в единстве Базы Знаний.

При формировании запроса к БЗ:

1. Строится семантическая сеть, отражающая структуру запроса.

2. Вывод обеспечивается за счёт сопоставления общей сети БЗ и сети для запроса.

Пример

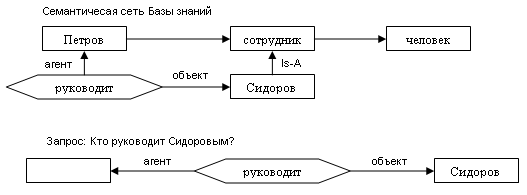
2.

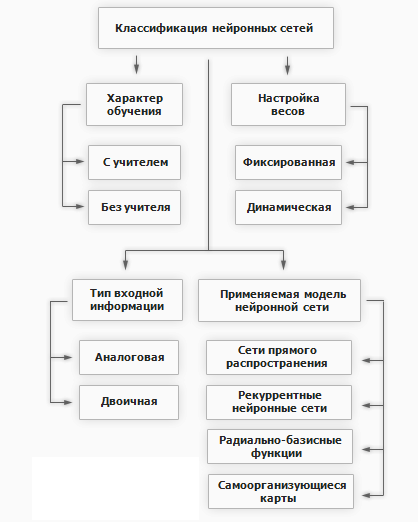
Характер обучения

Классификация нейронных сетей по характеру обучения делит их на:

нейронные сети, использующие обучение с учителем;

нейронные сети, использующие обучение без учителя.

Рассмотрим это подробнее.

Нейронные сети, использующие обучение с учителем. Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором. Далее веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемого уровня.

Нейронные сети, использующие обучение без учителя. Обучение без учителя является намного более правдоподобной моделью обучения с точки зрения биологических корней искусственных нейронных сетей. Развитая Кохоненом и многими другими, она не нуждается в целевом векторе для выходов и, следовательно, не требует сравнения с предопределенными идеальными ответами. Обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы.

Настройка весов

сети с фиксированными связями – весовые коэффициенты нейронной сети выбираются сразу, исходя из условий задачи;

сети с динамическими связями – для них в процессе обучения происходит настройка синаптических весов.

Тип входной информации

аналоговая – входная информация представлена в форме действительных чисел;

двоичная – вся входная информация в таких сетях представляется в виде нулей и единиц.

Применяемая модель нейронной сети

Сети прямого распространения – все связи направлены строго от входных нейронов к выходным. К таким сетям относятся, например: простейший персептрон (разработанный Розенблаттом) и многослойный персептрон.

Реккурентные нейронные сети – сигнал с выходных нейронов или нейронов скрытого слоя частично передается обратно на входы нейронов входного слоя.

Радиально базисные функции – вид нейронной сети, имеющий скрытый слой из радиальных элементов и выходной слой из линейных элементов. Сети этого типа довольно компактны и быстро обучаются. Предложены в работах Broomhead and Lowe (1988) и Moody and Darkin (1989). Радиально базисная сеть обладает следующими особенностями: один скрытый слой, только нейроны скрытого слоя имеют нелинейную активационную функцию и синаптические веса входного и скрытого слоев равны единицы.

Самоорганизующиеся карты или Сети Кохонена – такой класс сетей, как правило, обучается без учителя и успешно применяется в задачах распознавания. Сети такого класса способны выявлять новизну во входных данных: если после обучения сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну. Сеть Кохонена имеет всего два слоя: входной и выходной, составленный из радиальных элементов.

3.

Реализация эс с использованием нечеткой логики

Нечеткая ожидаемая переменная (Fuzzy expected value):

, где , , (1)

Пример

Дано 5 групп людей и известно значение функции χ для каждой группы, в данном случае характеристическая функция показывает степень распределения:

10 человек имеют возраст 20 лет → χ = 0.20, 20 человек имеют возраст 30 лет → χ = 0.30,

25 человек имеют возраст 45 лет → χ = 0.45, 30 человек имеют возраст 55 лет → χ = 0.55,

20 человек имеют возраст 60 лет → χ = 0.60

Получим следующие пять пар χ и μ:

(0.20, 1.00) (1.00 = [10+15+25+30+20]/100) – из 100 человек у 100 возраст >= 20 лет.

(0.30, 0.90) (0.90 = [15+25+30+20]/100)

(0.45, 0.75) (0.75 = [25+30+20]/100)

(0.55, 0.50) (0.50 = [30+20]/100)

(0.60, 0.20)

В соответствии с формулой (1) находим минимальную переменную для каждой пары:

min (0.20, 1.00) = 0.20, min (0.30, 0.90) = 0.30, min (0.45, 0.75) = 0.45,

min (0.55, 0.50) = 0.50, min (0.60, 0.20) = 0.20

Предполагаемый нечеткий возраст людей равен максимальному числу из этой выборки, т.е. 50 лет.

Нечеткий ожидаемый интервал (интервал нечетких переменных)

Нечеткий ожидаемый интервал (Fuzzy expected interval) был создан для случаев, когда применение FEV невозможно, т.е. если данные, полученные от пользователя, нечеткие.

Теорема 1. Заданы интервалы S = {s1,...,sn} и R = {r1,...,rm} такие, что .

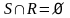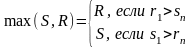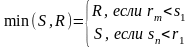Тогда (2), (3)

Теорема 2. Заданы интервалы S ={s1,...,sn} и R ={r1,...,rm} такие, что , , .

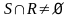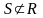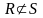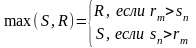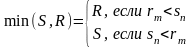Тогда (4), (5)

Теорема 3. Заданы интервалы S ={s1,...,sn} и R = {r1,...,rm} такие, что .

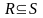Тогда max(S , R) = {r1,...,sn} (6), min(S , R) = {s1,...,rn} (7)

Пусть α и β – интервалы, тогда α выше β , если верхняя граница α выше, чем верхняя граница β.

Формулы для расчета верхней и нижней границ:

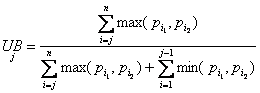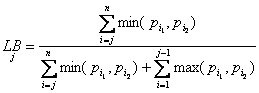(8) (9)

Экспертные системы, основанные на нечеткой логике. (нэс) Fuzzy expert systems

НЭС можно описать тремя логическими частями:

• The Front – end Compiler (FC) Конечный транслятор ( КТ )

• The Inference Engine (IE) Механизм вывода ( МВ )

• The Question-Answer Program (QAP) Модуль объяснений ( МО )

FC получает входные данные от пользователя или другой программы и компилирует их. Механизм вывода использует эти данные в форме продукционных правил.

У QAP только одна функция – следить за ходом решения и показывать результат.

Механизм вывода размещает данные в рабочей области. Каждый элемент рабочей области имеет:

• 2 – 3 ключевых слова;

• верхнюю и нижнюю границу переменных;

• фактор (не) уверенности, который используется для вывода решения;

• номер правила, которое, если предложение введено пользователем, равно 0, в противном случае – это номер из базы знаний.

Структура элементов рабочей области:

CF , когда данные введены пользователем, равны 1, даже если эти данные неопределенны (например, почти 30 человек имеют возраст от 20 до 25 лет).

Предложения, которые принимает FC :

5. сущ. им. падеж А + сущ. род. падеж B + глагол + прил. С

6. [ наречие ] +  [число до ] + число С

A и B – ключевые слова, C – ключевое слово и характеристика B.

Преобразование предложения первого типа опирается на значение прилагательного (глагол – это связка). Затем мы будем задавать значения, которые будут использоваться в утверждениях для механизма вывода. Отрицание будет вида «не С».

Пример 2

Отрицание: Цвет продукции не синий.

Для отрицания: [0… x - ε ][ x + ε ..1], ? = 0.01

Рабочая область:

Цвет продукции является синим.

Ключевые слова: цвет ( K 1), продукция

( K 2), синий ( K 3). Так как данные

введены пользователем, верхние и нижние

границы данного утверждения описываются

K 3. Так как K 3 – не число, то LB 1 = 0,

UB 1 = 1, LB 2 = UNDEF , UB 2 = UNDEF .

Рабочая область:

Нечеткое множество А характеризуется функцией принадлежности , которая ставит в соответствие каждому элементу число из интервала [0,1], характеризующее степень принадлежности элемента множеству А. Причем 0 и 1 представляет соответственно низшую и высшую степень принадлежности элемента к подмножеству А.

G – глобальное множество

– степень принадлежности

Точкой перехода нечеткого множества А называется элемент множества X, для которого .

Носителем нечеткого множества А называется четкое подмножество из X, на котором . В практических приложениях носитель – это чаще всего ограниченное множество.

Высотой нечеткого множества А называется максимальное значение функции принадлежности этого множества, то есть

Одноточечным нечетким множеством является множество, носитель которого состоит из одной точки. В дальнейшем мы иногда будем представлять нечеткое множество А как совокупность составляющих его одноточечных нечетких множеств:

Функция принадлежности может задаваться таблично или графически.

Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.

Лингвистической переменной называется набор (β, T, X, G, M), где

β - наименование лингвистической переменной;

T - множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X. Множество Т называется базовым терм-множеством лингвистической переменной;

G - синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество T G(T), где G(T) - множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;

М - семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество.

Чтобы охарактеризовать поведение системы и реализовать стратегию управления, нужно помимо описания с помощью лингвистических переменных всех важных параметров системы и внешних факторов также описать правила, по которым осуществляется связь между параметрами системы, внешними факторами и между параметрами и факторами.

Для представления правил используются продукционные правила (несколько посылок, одно заключение).