8.2 Символьное преобразование выражений

8. Упростить выражение

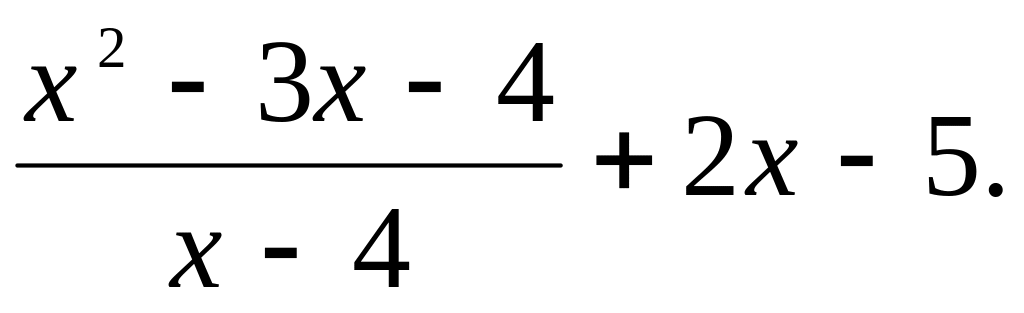
Рекомендации по выполнению

• Введите выражение и выполните команду Символы/Упростить (выделяющая рамка синего цвета должна полностью окружать выражение). Результат упрощения отобразится под выражением:

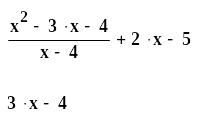
9. Упростить выражение (x + 2y)z – z² – (x + 5y) + z

Рекомендации по выполнению

• Откройте панель инструментов Символы кнопкой на панели Математика.

• Введите предложенное выражение и нажмите кнопку [Символ Упростить] на панели инструментов Символы (выделяющая рамка должна находиться внутри выражения), затем клавишу [Enter] или щелкните мышью вне рамки. Результат упрощения отобразится справа от выражения:

8.3 Работа с векторами и матрицами

10. Выполнить сложение, умножение и вычитание матриц А и В. Найти определитель, обратную и транспонированную матрицу для матриц А и В.

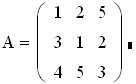
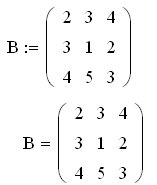
Рекомендации по выполнению

• Откройте панель инструментов Матрицы кнопкой на панели Математика.

• Создайте первую матрицу: наберите на экране А:= и нажмите кнопку [Создать матрицу или вектор] панели Матрицы. Задайте размерность матрицы в открывшемся окне: в поле Строки введите 3, в поле Столбцы – 3. Заполните шаблон матрицы.

• Аналогично создайте вторую матрицу.

• Найдите сумму, разность и произведение матриц. Для этого наберите выражения:

А+В= А-В= АВ=

• Вычислите определители матриц, получите обратные (инверсные) и транспонированные матрицы, воспользовавшись соответствующими кнопками панели Матрицы:

Примечание. Получить определитель, обратную, транспонированную матрицы можно и другим способом: полностью выделить матрицу и выполнить соответствующую команду меню Символы/Матрицы

11. Найти произведение заданного вектора V на константу 3:

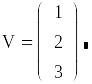
 Векторы являются частным случаем матриц размерности N1, поэтому для них справедливы те же операции, что и для матриц.

Рекомендации по выполнению

• Создайте вектор V как матрицу размерностью 3х1.

• Найдите произведение матрицы на константу, введя V3=

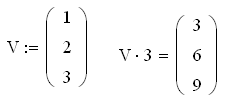
8.4 Решение уравнений

12. Решить квадратное уравнение x²+3x-4=0.

Рекомендации по выполнению

• Введите левую часть уравнения и выделите мышью переменную х.

• Выполните команду Символы/ Переменные/ Вычислить и получите результат:

13. Решить систему линейных уравнений:

 Для решения системы линейных уравнений воспользуемся матричной формой системы и применим метод обратной матрицы: систему линейных алгебраических уравнений вида A·Х=B умножим слева на матрицу, обратную матрице А:

A^-1·A·X=A^-1·B,

В результате система уравнений принимает вид:

E·X=A^-1·B,

где E – единичная матрица.

Таким образом, вектор неизвестных вычисляется по формуле:

X=A^-1·B.

Рекомендации по выполнению

• Создайте матрицу коэффициентов при неизвестных А размерностью 4х4 и матрицу свободных членов В размерностью 4х1:

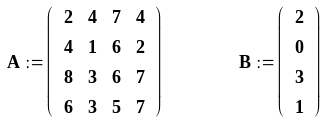
• Введите формулу вычисления вектора неизвестных Х для системы А·Х=В:

• Получите значения элементов Х, введя Х=

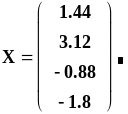
14. Определить объемы выпуска производственной фирмой продукции трех видов в условиях ограничения запасов ресурсов. Исходные данные приведены в таблице 8.1.

Таблица 8.1

Данные по выпуску продукции

Запасы ресурсов	Затраты на единицу продукции
	Продукция 1	Продукция 2	Продукция 3
24	5	7	4
75	10	5	20
10	5	2	1

 Имеем систему трех уравнений с тремя неизвестными.

Решим ее методом обратной матрицы.

Рекомендации по выполнению

• Выполните действия в порядке, аналогичном выполнению задания 13.

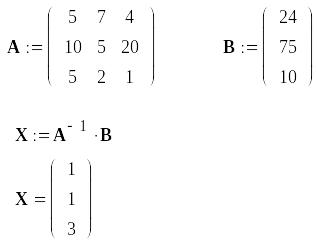
15. Решить нелинейное уравнение cos(x) = x + 0.2

 Для решения одного уравнения с одним неизвестным служит функция root (f(x), x), причем перед нею нужно задать начальное значение x.

Рекомендации по выполнению

• Приведите уравнение к виду f(x) = 0:

• Задайте начальное значение переменной х, равное 1:

• Найдите корень уравнения, введите root(f(x),x)= и получите результат:

Примечание. Можно функцию f(x) записать в функции root в явной форме:

16. Решить систему уравнений при начальных приближениях: x = 0; y = 1.

 Для решения системы уравнений служит вычислительный блок Given/Find. Он имеет следующую структуру:

Given (служебное слово, отмечающее начало блока)

Уравнения

Find(х,у,…)

Рекомендации по выполнению

• Откройте панель инструментов Булево кнопкой на панели Математика.

• Задайте начальные приближения:

• Введите с клавиатуры служебное слово Given, после него введите два уравнения системы, используя кнопку 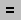[Булево равенство] на панели Булево, а затем наберите Find(x, y)= и получите результат: