27 Кванторы. Двухместные предикаты. Определения уравнения, тождества и неравенства.

Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих выcказывание. Чаще всего упоминают:

• Квантор всеобщности (обозначение: 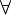, читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).

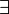• Квантор существования (обозначение: , читается: «существует…» или «найдётся…»).

пример

Обозначим предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные):

1. любое натуральное число кратно 5;

2. каждое натуральное число кратно 5;

3. все натуральные числа кратны 5;

следующим образом:

.

Следующие (уже истинные) высказывания используют квантор существования:

1. существуют натуральные числа, кратные 5;

2. найдётся натуральное число, кратное 5;

3. хотя бы одно натуральное число кратно 5.

Их формальная запись:

.

• Высказывание 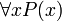означает, что область значений переменной включена в область истинности предиката .

(«При всех значениях (x) утверждение верно»).

• Высказывание 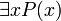означает, что область истинности предиката непуста.

(«Существует (x) при котором утверждение верно»).

Операции над кванторами

Правило отрицания кванторов — применяется для построения отрицаний высказываний, содержащих кванторы, и имеет вид:

Двухместный предикат – отображение, по которому каждой паре переменных указывается единственное значение 0 или 1.

Предикат  является двухместным предикатом, предметной областью которого могут служить любые множества действительных чисел. Высказывание истинно, а высказывание  ложно. Если вместо одной из переменных подставить число, то получится одноместный предикат.

28. Кванторные приставки о определение функции

Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих выcказывание. Чаще всего упоминают:

• Квантор всеобщности (обозначение: , читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).

• Квантор существования (обозначение: , читается: «существует…» или «найдётся…»).

Функция - х, у

Окружность - точка0, точка х, расстояние 0х одинаковое.

29. Понятие графа. Степень вершины графа. Ориентированные и неориентированные графы. Полный и пустой графы.

Граф – частный случай бинарного отношения, любая схема, на которой имеется изображение точек как-то связанных линиями.(схема трамвайных путей, ж/д, схема теплоснабжения и т.д.)

-это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).

Граф, или неориентированный граф  — это упорядоченная пара , для которой выполнены следующие условия:

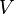• — это непустое множество вершин или узлов,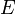

• — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

число вершин в графе  — порядком, число рёбер  — размером графа

Степенью вершины называется число ребер графа, которым принадлежит эта вершина.

Ориентированный граф - граф, рёбрам которого присвоено направление.

орграф D=(V, E) есть множество E упорядоченных пар вершин .

Дуга {u, v} инцидентна вершинам u и v. При этом говорят, что u — начальная вершина дуги, а v — конечная вершина.

Орграф, полученный из простого графа ориентацией ребер, называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.

йти к: навигация, поиск

Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с вершинами имеет рёбер и обозначается .

Пустой граф – граф степени 0, т.е. граф не содержащий ребер.