11 Определение функции. Композиция функции.

Функция (отображение, операция, оператор) — это закон или правило, согласно которому каждому элементу из множества ставится в соответствие единственный элемент из множества .

При этом говорят, что функция задана на множестве , или что отображает в .

Если элементу сопоставлен элемент , то говорят, что элемент находится в функциональной зависимости от элемента . При этом переменная называется аргументом функции или независимой переменной, множество называется областью задания или областью определения функции, а элемент , соответствующий конкретному элементу  — частным значением функции в точке . Множество всех возможных частных значений функции называется её областью значений или областью изменения.

Компози́ция фу́нкций — это применение одной функции к результату другой, сложная функция.

Пусть даны функции z=f(y) и y=g(x)

Композиция функции f и g называется отображение z→x (над стрелочкой fg )

z=fg(z)

свойства композиции

• Композиция ассоциативна:

.

• Если 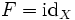— тождественное отображение на , то есть

,

то

.

• Если 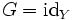— тождественное отображение на , то есть

,

то

.

12 Определение алгебраической операции и ее признаки.

На множестве А задана алгебраическая операция, если каждой упорядоченной паре (х, у) элементов х и у множества А поставлено в соответствие, по некоторому правилу, единственный для этой пары элемент . Говорят, что этот элемент есть результат алгебраической операции, примененной к паре (х, у) .

Алгебраическая операция – это отображение для которого выполняются следующие условия:

- всегда существует результат операции;

- этот результат единственный;

- этот результат должен принадлежать исходному множеству, на котором выполняется операция.

Сигнатура – набор операций, которые являются алгебраическими (N, +, *) (Z, +, -, *) (Q, +, -, *, : не равно 0)

Способы задания:

-формула

- таблица

- описание

- график

Свойства

1) Алгебраическая операция *, определенная на множестве А называется коммутативной, если она подчиняется закону коммутативности, т.е. для любых двух элементов х и у множества А выполняется равенство: х*у = у*х

2) Алгебраическая операция *, определенная на множестве А называется ассоциативной, если она подчиняется закону ассоциативности, т.е. для любых трех элементов х, у, z множества А выполняется равенство:

3) Пусть на множестве А определены две алгебраических операции, которые мы обозначим символами * и .

Операция * дистрибутивна относительно операции , если верны два равенства:

и .

13 Примеры унарных, бинарных алгебраических операций.

Алгебраическая операция называется унарной, если она производится с 1 элементом.

Унарной алгебраической операцией на множестве  называют соответствие, по которому каждому элементу  множества  сопоставляется определенный элемент  множества .

Например, унарной алгебраической операцией на множестве действительных чисел  является нахождение противоположного числа: для любого числа х=-х

Бинарная операция - бинарная алгебраическая операция определена на множестве, если всякой упорядоченной паре элементов множества М по некоторому закону ставится в соответствие вполне определенный элемент этого же множества.

Примеры: операция +/- на множестве Q( рациональных)

на множестве целых чисел являются сложение и умножение

Пусть — множество всех подмножеств множества . Операции пересечения и объединения — это бинарные алгебраические операции на множестве . Операция, ставящая в соответствие двум натуральным числам и их наибольший общий делитель НОД , является бинарной алгебраической операцией на множестве натуральных чисел.

Виды бинарных операций:

Бинарная алгебраическая операция на множестве называется коммутативной, если для всех .

Бинарная алгебраическая операция на множестве называется ассоциативной, если для всех .