37. Определение подграфа данного графа.

Подграф - граф, содержащий некое подмножество вершин данного графа и некое подмножество инцидентных им рёбер.

Порождённый подграф — подграф, порождённый множеством рёбер исходного графа. Содержит не обязательно все вершины графа, но эти вершины соединены такими же ребрами как в графе.

Подграф называется остовным подграфом, если множество его вершин совпадает с множеством вершин самого графа.

38. Определение объединения и пересечения графов.

Объединение графов.

 Пусть G1(V1,E1) и G’2(V’2,E’2) – произвольные графы. Объединением G1UG’2 графов G1 и G’2 называется граф с множеством вершин V1UV’2, и с множеством ребер E1UE’2. Свойства

  Объединение множеств является бинарной операцией на произвольном булеане 2^X;

  Операция объединения множеств коммутативна:

  Операция объединения множеств транзитивна (ассоциативность):

  Пустое множество X является нейтральным элементом операции объединения множеств:

  Таким образом булеан вместе с операцией объединения множеств является моноидом;

Операция пересечения множеств идемпотентна:

 Пересечение графов

 Пусть G1(V1,E1) и G’2(V2’,E2’) – произвольные графы. Пересечением G1∩G’2 графов G1 и G’2 называется граф с множеством вершин V1∩V’2 с множеством ребер E = E1∩E’2

Свойства

  Пересечение множеств является бинарной операцией на произвольном булеане 2^X;

  Операция пересечения множеств коммутативна:

  Операция пересечения множеств транзитивна (ассоциативность):

  Универсальное множество X является нейтральным элементом операции пересечения множеств:

  Таким образом булеан вместе с операцией пересечения множеств является абелевой группой;

  Операция пересечения множеств идемпотентна:

  Если — пустое множество, то

39. Определение дополнения графов

В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они не смежны в G.

Пусть G=(V,E) — простой граф и пусть множество K содержит все двухэлементные подмножества множества V. Тогда H=(V,K\E) является дополнением графа G.

Дополнением данного графа называется такой граф, сто их объединение дает полный граф.

40. Определение дерева и признак дерева.

Дерево – связные неориентированный граф, не имеющий цикла

- связный граф с минимальным количеством ребер, в котором вершин на 1 больше, чем ребер.

В дереве любое ребро является разрезом.

• Дерево не имеет кратных рёбер и петель.

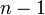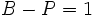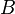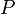• Любое дерево с вершинами содержит ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда , где  — число вершин,  — число рёбер графа.

• Граф является деревом тогда и только тогда, когда любые две различные его вершины можно соединить единственной простой цепью.

• Любое дерево однозначно определяется расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами.

• Любое дерево является двудольным графом. Любое дерево, множество вершин которого не более чем счётное, является планарным графом.

• Для любых трёх вершин дерева, пути между парами этих вершин имеют ровно одну общую вершину.