МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Институт неразрушающего контроля

Направление – Приборостроение

Кафедра – Физические методы и приборы контроля качества

ОТЧЕТ

по лабораторной работе №2

по курсу «Основы автоматического управления»

Динамические звенья второго порядка.

Выполнил студент гр.1Б01 Проничев Е.А

^{Подпись Дата И.О.Фамилия}

Проверил доцент каф. АиКС __________ В.П. Казьмин

^{должность Подпись Дата И.О.Фамилия}

Томск 2012

Цель работы:

Исследование переходных процессов, вызванных ступенчатым воздействием звеньях второго порядка, определение характера переходных процессов, типа корней характеристического уравнения и устойчивости звеньев.

Краткое теоретическое пояснение:

Динамические звенья второго порядка обладают большим количеством вариантов возможных выходных графиков, нежели звенья первого порядка. Это обусловлено тем, что в процессе вычисления корней характеристического уравнения используются комплексные числа.

Динамические звенья второго порядка можно условно разделить на:

• Апериодические звенья;

• Колебательные (периодические) звенья;

• Консервативные звенья.

Динамическое звено второго порядка можно описать дифференциальным уравнением в общем виде (1), передаточной функцией W(s) (2) и характеристическим уравнением (3):

, (1)

, (2)

. (3)

Вид графиков (сходящийся либо расходящийся, либо колебательный с постоянной амплитудой и частотой); характер переходного процесса (периодический либо апериодический); тип звена (апериодическое второго порядка, колебательное либо консервативное); устойчивость звена (устойчивое, неустойчивое, нейтральное) определяется корнями характеристического уравнения (3) (левые, правые, нулевые, вещественные, комплексные, мнимые).

Если корни уравнения (3) вещественные, S₁ = α₁; S₂ = α₂, то решение дифференциального уравнения (1) можно представить как сумму экспонент:

, (4)

где: , , ,

и звено в данном случае будет апериодическим второго порядка.

Если корни характеристического уравнения являются комплексно-сопряженными , то звено является периодическим (колебательным), а решение дифференциального уравнения можно представить в виде:

. (5)

Если в характеристическом уравнении , то звено является консервативным, при этом корни будут мнимыми

.

Ход работы

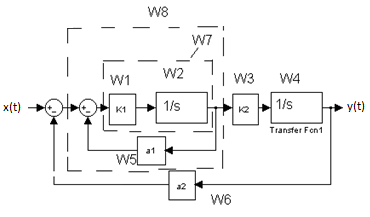
1. В программе Simulink создаем схему моделирования динамического звена второго порядка, изображенную на рисунке 1. Коэффициент передачи интегратора К_ин задаём равным 1.

1 .1 Пользуясь правилами структурных преобразований, для данной схемы получим выражения передаточной функции, характеристического уравнения и его коэффициентов , , .

; ;

После преобразования выделим W₇.

;

;

;

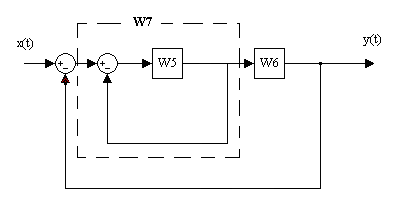
Зная общий вид уравнения передаточной характеристики, найдём соответствующие коэффициенты:

;

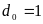; ; ; K=K₁K₂

Корни характеристического уравнения для данной передаточной функции имеют вид:

1.2 Рассчитаем диапазон изменения коэффициента , в котором переходный процесс является сходящимся апериодическим.

Для того, чтобы процесс был сходящимся апериодическим необходимо, чтобы дискриминант характеристического уравнения был большим либо равным нуля.

K₁²-4 K₁K₂≥0

Поскольку K₂ может принимать только положительные значения в данном случае, то диапазон его изменения будет иметь вид:

0 < K₂ ≤ (K₁)/4

1.3 Проверим результаты расчёта K₂ на модели Simulink. Для этого построим график переходного процесса.

Установим в схеме значения коэффициентов:К₁ = 1;К₂ = 0,25.

К₁ = 1; К₂ = 1

К₁ = 1; К₂ = 0,1

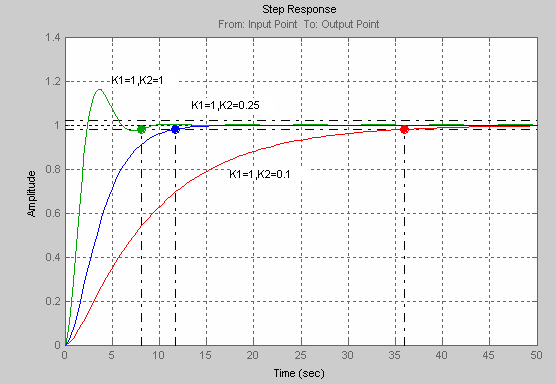
График1

Для К₂=0,25 соответствуют корни S₁=S₂=-0,5: корни отрицательные вещественные. Следовательно процесс устойчивый(сходящийся): условие выполняется.

Для К₂=0,1 соответствуют корни S₁= -0,887, S₂=-0,113: корни отрицательные вещественные. Следовательно процесс устойчивый(сходящийся): условие выполняется но время переходного процесса больше, чем при К₂=0,25.

Для К₂=1 соответствуют корни S₁=-0,5+0,866i, S₂=-0,5-0,866i:корни имеют мнимую составляющую. Процесс – периодический сходящийся: условие не выполняется

Рассмотрим переходные процессы для значений К₂, для которых корни характеристического уравнения являются левыми комплексными (процесс периодический сходящийся):

Установим в схеме значения коэффициентов:К₁ = 1;К₂ = 1

К₁ = 1; К₂ = 0,1

К₁ = 1; К₂ = 0,25

График 2

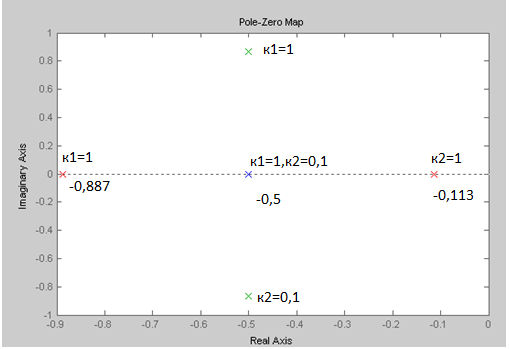
Для К2=0,25 соответствуют корни S1=S2=-0,5: корни отрицательные вещественные. Следовательно, процесс устойчивый (сходящийся): условие не выполняется.

Для К2=0,1 соответствуют корни S1= -0,887, S2=-0,113:корни вещественные. Следовательно, процесс устойчивый (сходящийся): условие не выполняется .

Для К2= 1 соответствуют корни S1=-0,5+0,866i, S2=-0,5-0,866i:корни имеют мнимую составляющую. Следовательно, процесс периодический сходящийся: условие выполняется

1.6 В программе Simulink создаем схему моделирования динамического звена второго порядка, изображенную на рисунке 6. Коэффициент передачи интегратора Кин задаём равным 1.

2.1 Пользуясь правилами структурных преобразований, для данной схемы получим выражения передаточной функции, характеристического уравнения и его коэффициентов , , .

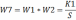
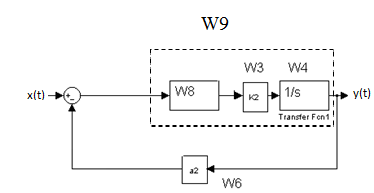
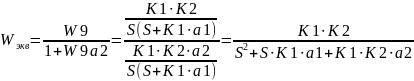
Характеристическое уравнение для этого динамического звена имеет вид:

=0, где

d₀= 1; d₁= К₁*a1; d₂= К₁* K₂*a2

Корни характеристического уравнения:

2.2 Рассчитываем значение коэффициента обратной связи 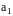при котором корни характеристического уравнения звена мнимые , а переходный процесс в звене имеет незатухающий колебательный характер с постоянной амплитудой и частотой.

Для осуществления такого переходного процесса, необходимо, чтобы:

К₁* K₂*a2>0;

К₁*a1=0. (зададимся а1=0, поскольку К1 задействован в верхнем выражении и не может быть равен нулю по условию)

Проверим данные условия на модели Simulink, зададимся К1=К2=1, а1=0 при изменяющемся а2.

График переходного процесса:

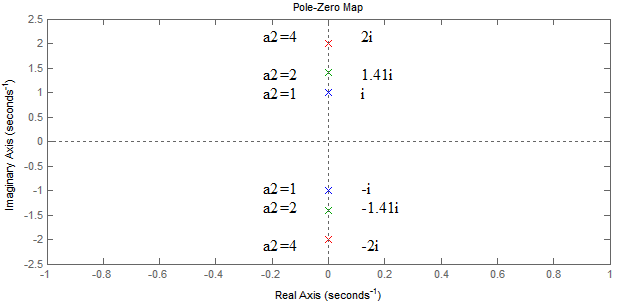
В данном случае из графиков можно заметить, что переходный процесс данного звена является незатухающим и имеет колебательный характер с постоянной амплитудой и частотой.

Поскольку корни характеристического уравнения имеют только мнимую составляющую, то можно сказать, что данное звено консервативное, а его устойчивость – нейтральна. По графику можно просмотреть, что с увеличением коэффициента а2 амплитуда и частота колебания уменьшаются, характер переходного процесса и его устойчивость не изменяются.