7. Римская система счисления.

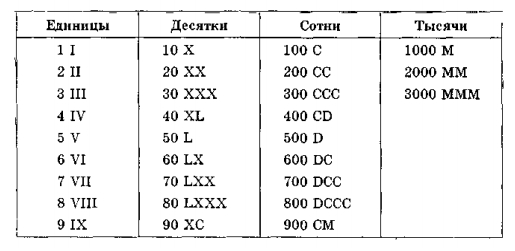
Числовые обозначения в Древнем Риме напоминали первый способ греческой нумерации. У римлян были специальные обозначения не только для чисел 1, 10, 100 и 1000, но и для чисел 5, 50 и 500. Римские цифры имели такой вид: 1 - I, 5 - V, 10 - X, 50 - L, 100 - C, 500 - D и 1000 - M. Возможно, знак V означал раскрытую руку, а X - две такие руки. Но есть и иное объяснение. Когда счет шел десятками, то, нарисовав 9 палочек, десятой их перечеркивали. А чтобы не писать слишком много палочек, перечеркивали одну палочку и писали десять так: . отсюда и получилась римская цифра X. А цифра 5 получилась просто разрезанием цифры для числа 10 пополам.

8. Восьмеричная и шестнадцатеричная системы счисления. В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

000 – 0

001 – 1

010 – 2

011 – 3

100 – 4

101 – 5

110 – 6

111 – 7

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифрации шестнадцатеричной системе счисления: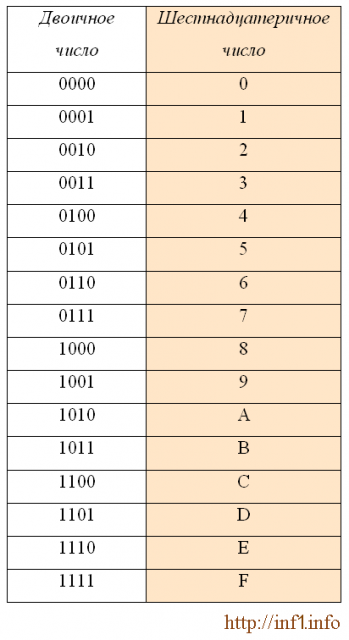

Например:

10001100101 = 0100 1100 0101 = 4 C 5 = 4C5

Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):

4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221

9. Общие правила превращения числа в другую систему счисления.

Существует несколько алгоритмов в решении данной задачи. Самый простой способ использует сложение и умножение. Суть задачи: записать число как равное ему в другой системе счисления с основанием р означает найти полином вида:

An-1*q^n-1+An-2*q^n-2+…+A₂*q²+A₁*q¹+A₀*q⁰

Преобразование методом Горнера

Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47. Перевод дробных чисел методом Горнера 1) 0,11012=0,X10

10. Превращение целых десятичных чисел в недесятичную систему счисления.

Хз