Тема 16. Обратная функция

Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией. Предположим, мы имеем функцию:

v = u 2 ,

где u - аргумент, a v - функция. Если поменять их ролями, то мы получим u как функцию v :

Если обозначить аргумент в обеих функциях через x , а функцию – через y, то мы имеем две функции:

каждая из которых является обратной по отношению к другой.

Тема 21. Степень с произвольным действительным показателем и её свойства. Преобразование и вычисление значений показательных выражений

Пусть a > 0, b > 0, r , s - любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.

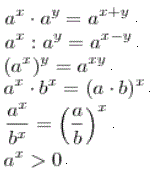
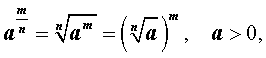
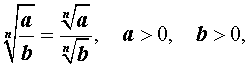
Тема 22. Выполнение тождественных преобразований над степенными выражениями

Равенство, обе части которого принимают одинаковые числовые значения при любых допустимых значениях входящих в него букв, называется тождеством. При выполнении тождественных преобразований алгебраических выражений нужно знать порядок выполнения действий, правила действий с дробями и степенными выражениями, формулы сокращенного умножения.

--- основное логориф. Тождество

Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b.

Тема 23. Логарифмы и их свойства

Логарифм положительного числа по основанию (обозначается ) — это показатель степени, в которую надо возвести , чтобы получить . b > 0, a > 0, а≠ 1.

Тема 25. Десятичные логарифмы.

Логарифм, взятый по основанию 10, носит название — десятичный логарифм.

Тема 27. Показательная и степенная функции, их свойства и графики

При a > 0, a = 1, определена функция y = a^ x , отличная от постоянной. Эта функция называется показательной функцией с основанием a.

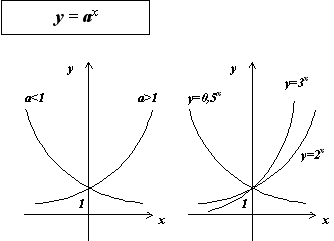
Основные свойства показательной функции y = a x при a > 1:

Область определения функции - вся числовая прямая.

Область значений функции - промежуток (0;+).

Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1< x2 , то ax1 < ax2

При x = 0 значение функции равно 1.

Если x > 0 , то a x > 1 и если x < 0, то 0 < a < 1.

Основные свойства показательной функции y = a x при 0 < a < 1:

Область определения функции - вся числовая прямая.

Область значений функции - промежуток (0;+).

Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1< x2 , то ax1 > ax2

При x = 0 значение функции равно 1.

Если x > 0 , то 0 < a < 1 и если x < 0, то a x > 1.

Степенная функция — это функция вида y = x p, где p — заданное действительное число.

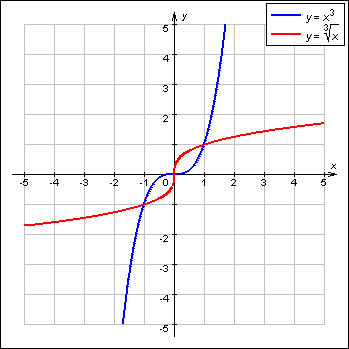
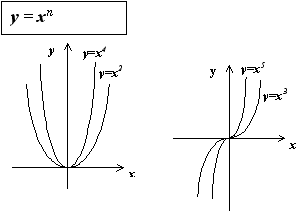
Тема 29. Показательные уравнения. Способы их решений

Основными методами решения показательных уравнений являются:

1.метод группировки и разложения на множители;

2.замена переменной.

Тема 31. Показательные и логарифмические неравенства.

Показательные уравнения

Простейшие показательные уравнения имеют вид:

Уравнение при и при корней не имеет, так как показательная функция всегда положительна.

1.

2.

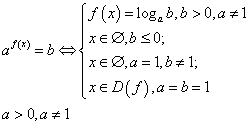
Если в уравнении присутствуют показательные функции с разными основаниями, можно попытаться привести их к одному и тому же основанию. То же относится и к логарифмическим уравнениям.

Логарифмические уравнения

Простейшие логарифмические уравнения имеют вид:

1.

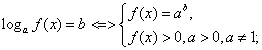
2.