Тема 8. Решение иррациональных уравнений

Иррацианальное уравнение – уравнение содержащие переменную под знаком корня. Что бы решить уравнение необходимо освободить от корней, подкоренное выражения которое содержит неизвестную величину. Иррациальное неравенство. При решении иррацианального неравенства не одной переменной необходимо свести его к решению равносильной системы рацианальных неравенств . Эти системы решаются при наложении ограничений на переменную и возведения обеих частей неравенства в одну и туже степень.

Тема 12. Способы задания функции.

Различают 3 способа задания функции:

1. табличный Состоит в простом перечислении элементов функции f, т.е. при этом способе указывается значение аргумента x и соответствующе значение функции y=f(x)

2. аналитический (формулы)

3. графический Область определения -- проекция данного графика на Ох, а множество значений -- проекция Д(f) на Оу.

ООФ(облось определения функции) называются ту значение которое могут принимать независимые переменые. Обозначается-D(Y)

Тема 13. График функции

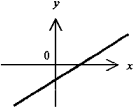
Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)

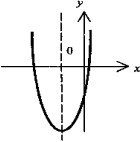
Парабола - график функции квадратного трёхчлена у = ах^2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0

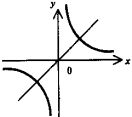
Гипербола - график функции у=а/х. При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0).

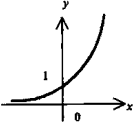
Экспонента (показательная функция по основанию е) у = е^x. (Другое написание у = ехр(х)). Асимптота - ось абсцисс.

Тема 14. Простейшие преобразования графиков функций

Параллельный перенос графика вдоль оси абсцисс на | b | единиц

вправо, если b > 0;

влево, если b < 0.

y = f(x + b) влево, если b > 0;

вправо, если b < 0.

y = f(x) + m Параллельный перенос графика вдоль оси ординат на | m | единиц

вверх, если m > 0,

вниз, если m < 0.

Отражение графика

y = f( - x) Симметричное отражение графика относительно оси ординат.

y = - f(x) Симметричное отражение графика относительно оси абсцисс.

Сжатие и растяжение графика

y = f(kx) При k > 1 — сжатие графика к оси ординат в k раз,

при 0 < k < 1 — растяжение графика от оси ординат в k раз.

y = kf(x) При k > 1 — растяжение графика от оси абсцисс в k раз,

при 0 < k < 1 — cжатие графика к оси абсцисс в k раз.

Преобразования графика с модулем

y = | f(x) | При f(x) > 0 — график остаётся без изменений,

при f(x) < 0 — график симметрично отражается относительно оси абсцисс.

y = f( | x | ) При x( >)0 — график остаётся без изменений,

при x < 0 — график симметрично отражается относительно оси ординат.

Тема 15. Монотонность, четность и нечетность, периодичность функций

Монотонная:

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).

Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2).

Чётная и нечётная:

Функция у = f (x) называется чётной, если она не меняется, когда независимое переменное изменяет только знак, то есть, если f (—x) = f (x). Если же f (—x) = — f (x), то функция f (x) называется нечётной. Например, у = cosx, у = x2— чётные функции, а = у sinx, у = x3— нечётные. График чётной функции симметричен относительно оси Оу, график нечётной функции симметричен относительно начала координат.

Периодичность функции:

Периодическая функция ― функция, повторяющая свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа