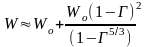3.4.3. Влияние температуры электролита

Если температура электролита отличается от стандартной (25^о С), обычно приводимой в литературе, то удельная электропроводность вычисляется по формуле:

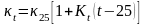
где 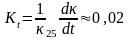- температурный коэффициент.

40. Падение напряжения в электролите с учетом газонаполнения

Многие электрохимические процессы сопровождаются образованием на электродах газовых пузырьков. Появление не проводящих электрический ток пузырей в межэлектродном пространстве приводит к:

• уменьшению эффективного поперечного сечения электролита между электродами и увеличению реальной плотности тока в электролите;

• огибанию пузырей линиями тока и увеличением длины пути тока между электродами.

Все это в целом, как следует из формулы закона Ома, обеспечивает увеличение падения напряжения в электролите.

где К – коэффициент увеличения сопротивления за счет газонаполнения; i_эф, L_эф - эффективные плотность тока и длина пути тока.

Коэффициент увеличения сопротивления электролита за счет газонаполнения зависит от величины газонаполнения и может быть рассчитан по следующим формулам:

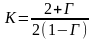
где Г – газонаполнение электролита.

Газонаполнение зависит от отношения объема газа в электролите к объему газожидкостной смеси:

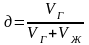
где V_г , V_ж - объем газовой и жидкой фаз, соответственно.

Величина газонаполнения зависит от многих факторов: удельной скорости газовыделения (плотности тока), скорости всплывания пузырей; также зависит от вязкости и плотности электролита межэлектродного расстояния и др. Кроме того, величина газонаполнения меняется по высоте электрода. Поэтому в расчетах пользуются полуэмпирическими формулами и упрощенными приближениями.

Количество газа, выделившегося между электродами площадью S, определяют по закону Фарадея:

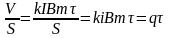
где q = kiВт, называется удельной скоростью газовыделения и обычно измеряется в см³/(см²с) , - среднее время нахождения пузырей между электродами.

Время нахождения пузырей между электродами зависит от высоты электродов Н и скорости всплытия пузырей W.

Время всплытия пузырей, выделяющихся на нижнем краю электрода, значительно больше, чем время всплытия пузырей, выделяющихся на верхней кромке электрода, где оно близко нулю. Поэтому принимают среднее время всплытия пузырей:

Высота электрода известна из конструктивного расчета, поэтому для расчета времени необходимо знать скорость всплытия пузырей.

40. Эксперименты показали, что скорость всплытия отдельных пузырей полностью соответствует формуле Стокса [12]:

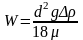
где d –диаметр пузыря; g – ускорение силы тяжести, _ж, _г - плотность жидкости и газа, _ж_г), - градиент плотности, может быть принят равным плотности жидкости;  - динамическая вязкость.

Эта формула отвечает ламинарному режиму всплытия пузырей. При всплытии достаточно крупных пузырей, скорость их движения возрастает пропорционально d² и режим их движения отличается от ламинарного. Для режимов движения, отличных от ламинарного, предложена формула:

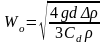
где С_d – коэффициент сопротивления среды, зависящий от числа Рейнольдса:

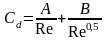
для 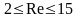А = 5,21 В = 13,1

А =41,9 В = 1,82

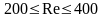А = 59,4 В = 0,082

Величину критерия Рейнольдса можно определить по величине критерия Архимеда:

где Аr – критерий Архимеда.

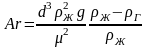
Максимальной скорости движения достигают пузыри диаметром 0,2 – 1,5 см. Она составляет около 30 см/с, и далее практически не зависит от размера пузырей. Это связано с деформацией пузырей и отклонением их формы от сферической.

При массовом всплытии пузырей их скорость определяется взаимодействием с жидкостью в приэлектродном пространстве. За счет вязкости раствора, пузыри увлекают его за собой и далее двигаются в потоке жидкости, направленном в сторону их движения. Скорость пузырей при этом увеличивается, и может быть определена по формуле Марручи [41]: