Введение

Первые серьезные исследования по геометрии в пространстве появились лишь в 30-х годах XVIII столетия. Прежде всего, Иоганн Бернулли вывел дифференциальное уравнение геодезической линии, затем в 1732 г. появилась работа Клеро, содержащая первые теоремы о пространственных кривых. В частности, в связи с вопросами геодезии, Клеро нашел геодезические линии на сфероиде, то есть на сжатом эллипсоиде вращения. Эйлер дал первые общие теоремы о кривизне поверхностей, а именно показал, что, какова бы ни была поверхность, если взять в какой-либо ее точке М нормаль к ней и рассматривать сечения поверхности плоскостями, проходящими через эту нормаль, то будет существовать одно сечение, у которого кривизна в точке М наибольшая, и другое, у которого кривизна наименьшая.

Гаусс проделывает огромную организационную работу и руководит измерением длины дуги меридиана от Геттингена до Альтоны и создает основы «высшей геодезии», занимающейся описанием действительной формы земной поверхности. Обобщающий труд «Исследования о предметах высшей геодезии» Гаусс создает в 1842-1847. В основе этого фундаментального труда лежат также принадлежащие Гауссу идеи так называемой внутренней геометрии поверхности, изложенной им в сочинении «Общие исследования о кривых поверхностях» (1827). Локальные (т. е. характеризующие малую окрестность точки) свойства поверхности, по мысли Гаусса, естественнее связывать не с «посторонними», введенными извне, а с внутренними криволинейными координатами и выражать через дифференциальную форму от внутренних координат. Если поверхность изгибать не растягивая, то ее внутренние свойства остаются неизменными. Впоследствии по образу и подобию внутренней геометрии поверхностей Гаусса была создана многомерная риманова геометрия.

Данная курсовая работа посвящена геометрической поверхности, называемая косым геликоидом. Цель работы: изучить геометрические свойства косого геликоида.

Необходимо решить следующие задачи:

• Найти параметрическое уравнение.

• Найти уравнение касательной плоскости.

• Найти уравнение нормали.

• Найти первую квадратичную форму.

• Найти вторую квадратичную форму.

• Найти нормальную кривизну.

• Найти индикатрису Дюпена.

• Найти полную и среднюю кривизны.

• Найти линии кривизны, асимптотические и геодезические линии.

• Найти деривационные уравнения поверхности.

Для решения поставленных задач нами были использованы классический метод исследования – метод дифференциальной геометрии.

Глава 1. Свойства поверхностей

1. Понятие о поверхности. Геликоид.

Множество точек евклидовой плоскости называется простой областью, если оно является образом открытого круга при его топологическом отображении; открытый круг, как известно, есть множество точек плоскости, лежащих внутри окружности. Множество Ω точек евклидова трехмерного пространства именуется простой поверхностью, если оно есть образ простой области Φ при ее топологическом отображении в . Пусть u, v- декартовы координаты точки области Φ, а x, y, z – декартовы координаты соответствующей точки простой поверхности Ω. Тогда

x=x(u,v), y= y(u,v), z=z(u,v) (1.1)

Равенства (1.1) называют уравнениями поверхности Ω в параметрической форме. В векторном виде:

(1.2)

Множество Ω точек мы будем называть регулярной поверхностью класса , если любая точка множества Ω имеет окрестность U, которая является простой поверхностью, представимой уравнениями (1. 1) (все три функции x(u,v), y(u,v), z(u,v) принадлежат к классу , т.е. имеют непрерывные производные до порядка k включительно, при k=1 имеем гладкую поверхность). В силу требования, чтобы u взаимно однозначно и взаимно непрерывно отображалась на простую область в , матрица

(1.3)

должна иметь ранг, равный 2, или, что то же, радиус-вектор поверхности должен в окрестности U удовлетворять условию

( ) . (1.4)

Точки поверхности Ω, в которых в нарушение условия (1.4) векторы коллинеарны, именуются особыми точками параметризации поверхности.

Если во всех точках окрестности U соотношение (1.4) неверно, т.е. , то ранг матрицы (1.3) не превышает 1. Если =1, то, как доказывается в математическом анализе, среди переменных x, y, z две будут функциями от третьей, и вместо поверхности мы будем иметь линию. Если же =0, то x, y, z постоянны, и мы имеем точку.

Если поверхность задана уравнением (1.1), то говорят, что она задана параметрический.

Параметризация поверхности изменится, если мы положим:

(1.5)

И выразим с помощью (1.5) как функцию от новых параметров , . Чтобы сохранить класс регулярности поверхности, мы должны потребовать, чтобы обе функции и также принадлежали к классу , т.е. имели непрерывные производные до k-го порядка включительно. Кроме того, для разрешимости уравнений (1.5) относительно u и v необходимо, чтобы функции φ и были независимы, для чего, как известно, должно быть выполнено условие:

(1.6)

( - сокращенное обозначение для и т.д.).

Если условие (5.6) верно в какой-либо точке P поверхности, то в силу непрерывности функций и оно будет справедливо и в некоторой окрестности V точки P. В этой окрестности в новой параметризации поверхность S будет снова простой и сохранит свой класс регулярности.

Гомеоморфизм, отображающий по формулам (1.1) простую поверхность Φ на простую поверхность Ω, именуется параметрическим представлением поверхности Ω. Изменяя параметризацию на основе формул (1.5), мы получим другое параметрическое представление той же поверхности Ω. Два указанных представления считаются эквивалентными, если во всей области Φ выполнено условие (1.6) и в (1.5) обе функции и принадлежат классу . Таким образом, простая поверхность Ω представляет собой класс эквивалентности, содержащий все эквивалентные друг другу ее параметрические представления.

Если, в частности, при параметрическом задании поверхности u=x, v=y, то у нас налицо явное задание поверхности

z= f(x, y) (1.7)

как известно из математического анализа, если матрица (1.3) имеет ранг, равный 2, или, иначе говоря, если по меньший мере один из определителей

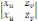, , , (1.8)

скажем первый из них, отличен от нуля в данной точке P, то первое и второе из уравнений (1.1) определяет в некоторой окрестности точки P, U и V как функции от x, y:

u=u(x, y), v=v(x, y). (1.9)

Подставляя выражения для U, V из (1.9) в третье из уравнений (1.1), найдем

z=f(x, y).

мы видим, что параметрическое задание поверхности всегда может быть сведено (в достаточно малой окрестности) к явному заданию; обратно, явное задание есть частный случай параметрического (u=x, v=y).

Часто применяется еще и неявное задание поверхности, т.е. задание ее уравнения вида

F(x, y, z)=0, (1.10)

где, F принадлежит классу , k . Если хоть одна из производных , например, , отлична от нуля в данной точке P, а следовательно, в ее окрестности U,то, как известно из теории неявных функций, в окрестности U координата z есть функция от x, y:

z=f(x, y),

причем функция f находится в том же классе . Таким образом, и неявное задание поверхности может быть сведено (в достаточно малой окрестности) к явному.

Точка поверхности (1.10), в которой

=0, (1.11)

называется ее особой точкой.

Геликоидом называется поверхность, образованная движением прямой AB, которая пересекает неподвижную прямую OZ (ось геликоида) под прямым углом, вращается около этой оси и в то же время смещается вдоль нее на расстояние, пропорциональное углу поворота (рис. 1.1). За криволинейные координаты точки M геликоида мы можем принять

1) ее расстояние u=MA до оси и

2) угол v поворота образующей AM, отсчитываемой от некоторого начального положения.

Отнесем геликоид к прямоугольной системе координат, приняв его ось за ось Z, а начальное положение образующей - за ось X. Тогда

x=OQ=OPcosv=MAcosv=ucosv,

y=QP=usinv.

Согласно условию, путь OA, пройденный точкой A по оси, пропорционален углу v, и мы можем положить z=OA=av, где a («ход геликоида») есть смещение образующей при повороте ее на один радиан. Итак, параметрические уравнения геликоида имеет вид:

x=ucosv, y=usinv, z=av. (1.13)

Р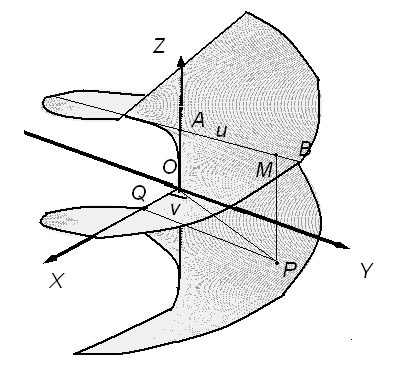 ис. 1.1.