I. Поверхностные модели

Описывают поверхность трехмерного объекта

а) полигональные сетки

б) параметрические (бикубические) поверхности

а) сетка – совокупность плоских многоугольников

если объект обладает криврлинейной поверхностью, то несколько плоских многоугольников

б) поверхность описывается в виде 3^х уравнений для х, у, z. Каждое уравнение зависит от двух параметров, степень при каждом параметре не выше третьей  бикубические поверхности.

Граница бикубической поверхности – параметрическая бикубическая кривая.

Класс кривых поверхностей относится к сплайновым кривым.

Сплайн (металическая линейка) – что-то типа ликало.

Сплайновая кривая.

Недостаток: более сложный математический аппарат, особенно в области определения невидимости.

Плюсы:экономия появляется при описании кривой поверхности.

Поверхностные модели нельзя применить в прозрачных моделях.

II. Модели сплошных тел.

Объект описывается как физическое тело.

Самая простая ячеичная модель – трехмерный аналог растрового изображения.

Минусы: огромное количество памяти для описания объекта.

III. Модель сплошных конструктивов.

Объекты строятся как совокупность примитивов. Примитивы либо плоские, либо ограничены несколькими плоскостями, либо ограничены поверхностями второго порядка – цилиндры, конусы и т.д.

Над примитивами выполняются операции: объединение, суммирование, вычитание, пересечение.

Следующий элемент реалистичного изображения:

2) Окрашивание объектов.

Положение источников света отосительно объекта наблюдения, окрасить в зависимости от взаимного расположения источника света и объекта.

И сточники света.

точечные распределенные

(дневные лампы)

3) Передача глубины.

Способы:

1. Передача глубины яркостью. (чем дальше объект, тем меньше его яркость)

2. Отсечение по глубине. Линии, уходящие в даль отсекаются.

4) Стереоскопия

Смысл: Восприятие объекта как трехмерного за счет расстояния между глазами.

На устройстве формируется 2 раздельных изображения для левого и правого глаза – это стереоизображения. Самый простой способ – стереоочки.

Полигональные сетки.

Это совокупность вершин, ребер и плоских многоугольников.

Возможно несколько способов описания полигональной сетки: универсального способа не существует.

Критерии для выбора способа описания:

1. объем памяти

2. простота формирования изображения

3. простота поиска многоугольника по ребру и наоборот

4. простота нахождения общих вершин для многоугольника.

5. простота поиска ошибок в описании

I способ. Явное описание многоугольников

Каждый многоугольник задается списком вершин:

Вершины задаются в некоем порядке (по часовой или против часовой стрелки).

Плюсы: - для каждого отдельного многоугольника эффекотвно ????

Минусы: отсутствует явное описание общих вершин для нескольких многоугольников. Чтобы найти вершины нужно проссмотреть все коор-ные тройки  вследствие машинного округления вершину можно вообще не найти.

• информация о вершинах дублируется

II. способ. Задание многоугольников с помощью указателей на список вершин.

Информация хранится один раз (один список вершин).

Каждая вершина описывается один раз  экономия памяти. Легко организовать перемещение вершины. Многоугольник рисуется соединением соответствующих вершин, некоторые ребра рисуются дважды.

Нет явного описания общих ребер.

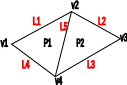
III. способ. Явное задание ребер.

Имеется список вершин, многоугольник описывается как список указателей на ребра, каждое ребро описывается бвумя вершинами:

Р₁ , Р_» - либо пусто, либо указатели на многоугольник.

Уравнение плоскости с помощью полигональной сетки:

Вектор нормали к плоскости: