Алгоритм Брезинхейма рисования отрезка.

Уравнение отрезка :

Выбираем целочисленный x ., решаем уравнение, получаем Y.

Решение требует ???? умножения  долго рисует.

Подход: пусть необходимо на каждом шаге выбрать точку, максимально близкую к изображаемому объекту. Подход состоит в том, чтобы произвести оценку расстояния до ближайших точек и выбрать точку, расстояние до которой будет минимальным.

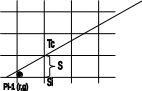
Или (x_i-1,y_i-1)

Пусть отрезок идет от точки x1 y1 до точки x2 y2.

Для начала x1=0 y1=0

 наклон отрезка меньше 45⁰

Расстояние от отрезка до T_i – t

от отрезка до S_i – s

используется для принятия решения:

если  0, то S t и будем брать нижнюю точку.

если 0 , то S t и будем брать верхнюю точку.

Умножаем все на dx:

- положительная величина  на знак разности не влияет 

- используется для принятия решения

нижняя точка

верхняя точка

из (2) – (1):

т.к. коор-ты дискретные

если , то выбираем нижнюю точку.

Тогда

если , то верхняя точка

из (2) 

Алгоритм впервые разработан для графопостроителя

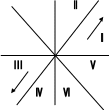
Алгоритм для области I

Для области II –x и y меняются местами

Область III прелбразовывает обл. I, если начальную и конечную точки отрезка поменять местами.

I V – тоже II , но начальную и конечную точки меняем местами.

V от I и II

VI знак одной из коор-т меняется на противоположный.

Рисование окружности методом Брезинхейма.

Уравнение окружности:

Окружность обладает восьми сторонней симметрией. Можно строить только четвертушку. Мы оцениваем расстояние от точки до окружности и выбираем минимальное.

Точку Р выбрали как ближайшую к окружности на предыдущем шаге. На следующем шаге следующие точки, которрые будем рассматривать как ближайшие.

Окружность может проходить по 1 из 5 траекторий.

Расстояние от точки до окружности

Для Т:

Если , то точка S длиже к окружности, чем точка Т и нужно брать S.

Вводим управляющую переменную:

Если , то берем S

Если , то берем Т

Возьмем случай С (см.рисунок) – S снаружи , , т.к. внутри окресности:

(*)

Возьмем случай А и В - нужно брать точку S :

Случай Е и D :  из (*) и правильно берем точку Т.

Для всех случаев можно брать (*).

Для первого шага:

Если , то точка S

Если , то точка Т

Если , то

Если , то

Компьютерные шрифты.

Шрифт в КГ уникальное явление. Шрифтом мы пользуемся при воспроизведении и восприятии информации. Шрифт – способ кодирования информации, служащий для передачи её в виде изображения. Шрифт представляет из себя набор символов, объединенных языковыми и художественными особенностями. При появлении книгопечатания появились шрифты. Шрифт как система кодирования обладает следующими свойствами:

1. В шрифтах, относящихся к одному языку данному символу соответствует только один набор существенных характеристик.

2) Для облегчения восприятия символы, относящиеся к одному шрифту, должны иметь одинаковый элемент (последние символы должны быть легко - читаемы).