Независимость пакета от графических устройств.

1 Способ обеспечения независимости.

Слой абстрактной аппаратуры

Пр. Direct Draw

2.

На низкоуровневом

языке

Замкнутая, не зависящая от устройства, низкоуровневая прог-ма описания картинки наз. метафайлом.

Пр.HPGL- графический язык.

Геометрические преобразования.

Двумерные преобразования.

Двумерный перенос:

т. Р(x,y) перенос в т. P^’(x^’,y^’)

Двумерный перенос можно описать:

x^’ = x+Dx

y^’ = y+Dy

О бозначим P = [x,y] , P^’=[x^’,y^’]

P^’=P+T (1)

T= [D_x,D_y]

Масштабирование точки относительно начала координат.

x^’ = S_x*x , где S_x –масштабир. множитель.

Y^’ = S_y*y

О бозначим

S= S_x 0 масштабирование в матричном виде: P^’=P*S

(2)

0 S_y

Поворот точки Р относительно начала координат на угол .

Y

P^’ P: x=r*cos 

Y=r*sin 

P P: x^’=r*cos(+)=r*coscos - r*sinsin=

R =x*cos - y*sin

 y^’=r*sin(+) = x*sin + y*cos



X

Обозначим:

R=  sin

-sin  cos поворот относительно начала коор-т

P^’=P*R (3)

В комп. графике существует система однородных коор-т: двумерн. одонородные коор-ты: (X,Y,W) соотношения:

x= ; y=

Е сли это не оговаривается, то масштаб. коофициент W=1 и (x,y,1)

Перенос точки можно осуществить с помощью матрицы вида:

1 0 0

Т= 0 1 0

D_x D_y 1

Е сли P=[x,y,1], P^’=[x^’,y^’,1] перенос в однород. коор-тах: P^’=P*T(D_x,D_y) (4)

Если имеется точка Р, которая переносится в точку Р^” на расстоянии D_x1,D_y1, затем Р^’ в Р^’’ на расст. D_x2, D_Y2.

P^’=P*T₁, P^’’= P^’ T₂= P* T₁* T₂

1. 0 0 1 0 0 1 0 0

0 1 0 * 0 1 0 = 0 1 0

D_X1 D_Y11 D_X2 D_Y21 D_X1+D_X2 D_Y1+D_Y2 1

Подобное матричное произведение называется композицией преобразований.

Масштабирование в однород. коор-тах записывается в виде матрицы:

S_X 0 0

S= 0 S_Y 0 и уравнение масштабирования: P^’= P*S(S_X,S_Y) (5)

0 0 1

Поворот:

cos sin 0

sin cos 0

0 0 1

Пример. Повернуть квадрат относительно точки Р на угол .

Разбиваем на 3 подзадачи:

1. переносим точку Р в начало координат

2. поворачиваем вокруг начала коор-т

3. возвращаем на место

1) описываем с помощью матрици Т(-x,-y)

2) R()

3) T(x,y)

Р(x,y)

T(-x,-y) * R() *T(x,y) = M , M- суммарная матрица преобраэований

Ко всем точкам изображения применяем матрицу М : Р_I^’ = P_I * M

Композиция общего вида будет иметь результирующую матрицу вида:

₁₁ ₁₂ 0

₂₁ ₂₂ 0

t₁ t₂ 1

суммарный суммарный перенос

поворот и

растяжение

Умножение на матрицу: x^’=xr₁₁+yr₂₁+t₁

y^’=xr₁₂+yr₂₂+t₂

Для преобразования одной двумерной точки нужно 4 умножения, 4 сложения.

x^’=xcos-ysin

Если нужно быстро поворачивать на какой-либо небольшой угол, то cos≈1 

x^’=x-y*sin 

y^’=x*sin - y (но в этом случае будет накапливаться ошибка )

В общем случае произведение матртц – операция не коммутативная, поэтому при матричном произведении нужно отслеживать порядок матриц.

Существует операция, где этот порядок не важен:

• 2 последних поворота

• 2 последних переноса

• 2 последних масштабирования

• однородное масштабирование и поворот

Трёхмерные преобразования.

Будем рассматривать как расширение двумерных преобразований.

В двумерном случае положительным считается поворот от 0 к OY.

В трёхмерном положительным считается поворот, который, если смотреть с положительного конца оси, переводит одну положительную полуось в другую: OXOY, OYOZ,OZOX.

Если положительные повороты против часовой стрелки, то система коор-т называется правосторонней.

В комп. графике чаще применяется левосторонняя система коор-т: ось Х направлена вдоль нижней границы экрана вправо, Y – вдоль нижнего края вверх, Z – вглубь экрана (Z-как расстояние от экрана до объекта).

Вводим однородные коор-ты: описывание 3-хмер. точек в виде четвёрки (X,Y,Z,W).

Y

Z

X

Матрица 3-хмер. преобразований:

1. 3-хмер. перенос

1 0 0 0

0 1 0 0

0 0 1 0

P_XP_YP_Z1

2. 3-хмер. мастабирование

S_X 0 0 0

0 S_Y 0 0

0 0 S_Z0

0 0 0 1

3. поворот (вокруг оси Z):

cos sin 0 0

R_Z= -sin cos 0 0

0 0 1 0

0 0 0 1

вокруг оси Х:

1 0 0 0

R_X= 0 cos sin 0

0-sin cos 0

0 0 0 1

вокруг оси Y:

cos 0 -sin 0

R_Y= 0 1 0 0

sin 0 cos 0

0 0 0 1

Произвольная последовательность 3-хмер. преобразований:

r₁₁ r₁₂ r₁₃ 0 ортоганальная матрица, единицы –

M= r₂₁ r₂₂ r₂₃ 0 единичные вектора, в которые

r₃₁ r₃₂ r₃₃ 0 перейдут орты коор-ных осей

t₁ t₂ t₃ 1 после поворота.

x^’= xr₁₁+ yr₂₁+ zr₃₁ (9 умножений, 9 сложений)

y^’= xr₁₂+ yr₂₂+ zr₃₂

z^’= xr₁₃+ yr₂₃+ zr₃₃

Для ортоганальной матрицы обратная матрица получается путем транспонирования исходной.

Изображение 3-хмер. объектов.

Большинство устройств плоские. Механизм, который переводит 3Д объект в 2-мерн. изображение называется проекцией. Изображение строится на плоскости. Из центра проекции опускаются линии, которые называютя проекторами. Проекторы проходят через точки объекта, и находим пересечение линий с картинной плоскостью.

В зависимости от расстояния между центром проекции и картинной плоскостью выделяется 2 класса проекций:

1. если расстояние бесконечно, проекторы – параллельные линии, проекция – параллельна.

2. если расстояние конечно, проекторы сходятся в одной точке, проекция называется центральной.

1. 2

   * А^э

   *D

   В^э

   )

В

*

А *С

Класификация проекций.

П араллельные проекции

ортографические косоугольные

ортоганальные аксонометрические

Ортографические проекции – такие, в которых проектор с картинной плоскостью составляет прямой угол.

Косоугольные – угол произвольный.

В ортогональных проекциях картинная плоскость совпадает с одной из коор-ых плоскостей.

3 вида: вид спереди, вид сзади, вид сверху.

Информация о коор-тах точек вдоль одной из коор-ых осей теряется полностью.

В оксонометрических проекциях углы между картинной плоскостью и направлениями коор-х осей не прямые и вид проекции зависит от соотношения этих углов. Если все углы одинаковые, то проекция называется изометрией. Есть всего 8 направлений, где углы будут равны; изометрических проекций всего 4.

Диметрия – направление проецирования с 2 осями составляют одинаковый угол. Все рассьтояния вдоль двух осей искажены одинаково, вдоль третьей нет.

Триметрия – все три угла различны.

Косоугольная проекция:

1 - угол между напрвлением проецирования и акртинной плоскостью равен 45^О проекция называется фронтальной косоугольной диметрией или кабинетной проекцией (Cabinet).

2 – Cavalier – косоугольная изометрия.

Центральная проекция пучка параллельных прямых сходится в одной точке – точке схода. (Пр. дорога).

Если пучок прямых параллелен одной из коор-ых осей, их точка схода называется главной. Коор-х осей три  три класса проекций: одноточечная, двухточечная, трехточечная – сходятся линии вдоль всех осей.

Математический аппарат плоских геометрических проекций.

Есть точка Р [x,y,z,1]

1) Ортогональная проекция:

1 0 0 0

М_орт= 0 1 0 0

0 0 0 0

0 0 0 1

Р*М_орт=Р^”

Любую ортографическую проекцию можно свести к ортоганальной .

2) Центральная проекция.

Пусть центр проекции находится в начале координат. Пусть операция проецирования производится в левосторонней экранной системе коор-т. Изображение строится на плоскости, которая перпендикулярна оси Z и находится на расстоянии d от начала коор-т.

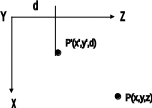
P’ – проекция Р

Матрица проекций:

Второй случай центр. проекции – коор-я плоскость совпадает с плоскостью XY, а центр. проекция лежит на расстоянии d от начала коор-т.

Два подобных треугольника

По аналогии матрица проецирования:

3) Проекция наиболее общего вида: параллельная проекция.

Плоскость зададим опорной точкой (VRP) и нормалью к картинной плоскости (VPN)

Нужно задать видимый объем, произвести отсечение по его границам, спроецировать что осталось на картинную плоскость, отобразить примитивы на поле вывода (как в двумерном случае).

Видимый объем частично задается окном на картинной плоскости. Чтобы задать окно, на картанной плоскости вводим систему коор-т UV. Вводим вектор вертикали, который показывает, где у этой картины вертикаль вверх (VUP).

Ось V – проекция вектора вертикали

на картинную плоскость , а ось U

выбирается так, чтобы U,V и VPN

образовывали левостороннюю сис.

коор-т. Задаем в этой сист. коор-т

окно, кот. огранич. объем по бокам.

направление проекции

Окно задает верхние, нижние и боковые границы. Введем 2 секущие плоскости: заднюю и переднюю.

Отсечение по границам объема будет производиться легче, если его привести к некоторому единичному виду. Для ортогональной проекции приведем объем к виду единичного куба. x=0, x=1, y=0, y=1, z=0, z=1.

Для центр. : к виду единич. куба.

x =-z, x=z, y=-z, y=z, z=1, z=z_MIN.

Эти объемы называются каноническими.

Наша задача - произвольный видовой объем привести к каноническому виду для улучшения проецирования. Приведение к каноническому виду для случая параллельной проекции состоит из следующих шагов:

1)опорную точку VRP переносим в начало коор.

2)поворот, при котором направление VPN

совпадает с отриц. направлением оси Z.

1) 2)

3) Поворот, при котором проекция вектора вертикали на картинную плоскость совпадает с осью Y.

4. Переход от правосторонних ?? коор-т к левосторонним экранным.

5. Если проекция косоугольная, то нужно ось видимого объема сдвинуть так, чтобы она была параллельна оси Z.

6. Смасштабировать видимый объем до единичного куба.

1)

2)3) комбинация произвольной последовательности поворотов есть матрица:

VPN совпадает с отрицательным направлением

оси Z .

ортогональная матрица: то, во что переходит ось Z после поворота.

нормируем

- векторное произведение

4):

Е сли проекция косоугольная, то видимый объем имитирует вид косоугольного параллепипеда:

Пусть изначально направление проецирования задавалось вектором DOP.

Вектор

DOP – направление проецирования.

6) : Масштабирование

6.1) Нужно сделать так, чтобы один из углов объема совпал с началом коор-т:

6.2) Сжать до единичного куба

видимый объем ограничен плоскостями

Для центральной проекции.

1. Перенос центра проекции в начало коор-т

2. Поворот, при котором направление нормали картинной плоскости совпадает с отрицательным направлением оси Z.

3. Проекция вектора вертикали на картинную плоскость совпадает с осью Y.

4. Переход к левосторонней системе коор-т

5. Сдвиг, при котором ось вид. объма совпадает с осью Z

6. Масштабирование.

1)2)3)4) как для параллельного

5 ) :

Ось вид. объема проходит через центр окна, и в системе коор-т UV центр окна имеет коор-ты:

В мировой системе коор-т:

6 ) :

Сжать объм до канонической пирамиды

Матрица сжатия:

, - расстояние до задней секущей плоскости

Отсечение:

Модифицированный алгоритм Сазерленда-Коина дла отсечения по границам канонического 3-хмерного объема: концам отрезка ставим в соответсвие 6-тимерный код вне/внутри. Отдельные биты вычисляются следующим образом:

Бит1=1, если точка выше вид. объема

Бит2=1, если -------- ниже-------------------

Бит3=1, если --------правее ----------------

Бит4=1, если --------левее ------------------

Бит5=1, если --------позади -----------------

Бит6=1, если --------впереди----------------

Запишем отрезок в параметрическом виде:

Для верчней грани:

Если , то точка пересечения отрезка с верхней гранью лежит за пределами куба

Точка выше объема, если

ниже

На верхней грани этой самой пирамиды , если , то находим коор-ту y и коор-ту x.

Основные растровые алгоритмы.

Архитектура растровых дисплеев.

Основой растровых дисплеев является ЭЛТ – электронно-лучевая трубка. Принципиально устройство ЭЛТ не отличается от осциллографа.

Цветные кинескопы 2-х видов:

1. С двух уровневым возбуждением 2 слоя люминисцир. вещества, 2 слоя с разной энергией возбуждения .

Современный цветной кинескоп: есть 3 катода, на экране люминофор 3-х цветов: красного, зеленого, синего. По способу возбуждения люминофоров кинескопы делятся на 2 вида:

• д ельтовидный

Экран покрыт пятнами. Между катодом и пятнами – теневая маска, чтобы луч только на своё пятно светил.

Минусы: 1) расстояние между щелями теневой маски ограничено.

2 ) Теневая маска поглащает очень много энергии скорость не очень и т.д.

• п ланарный

Щелевая маска – щели вертикальные.

Свойства цветного кинескопа:

1 ) сведение – 3 луча должны сводиться в одну точку видимая граница между черным и белым не должна иметь цветной зацветок в одну и другую сторону.

2. линейность – вертикальная линия вертикальна по всему экрану, гризонтальная аналогично.

Параметры телевизора:

1) Частота кадровой развёртки – количество кадров, которые выводятся в секунду на нашем телевизоре.

50 Гц – на бытовом телевизоре, комп. телевизоре 70-75 Гц , чтобы изображение не мерцало.

Бывает построчная развёртка и черезстрочная развёртка (сначала четная , потом нечетная)

2) Частота строчной развертки определяет количество строк, выводимых на экране в единицу времени, n.

3) Полоса пропускания – самая высокая частота в видео сигнале – грубо: частота строчной развертки X количество точек в одной строке.

Набор частот, кадровых и строчных, может быть фиксирован или динамически меняться от параметров входящего видео сигнала(мультичастотный монитор)

С точки зрения программы растровые дисплеи – дисплеи, отраженные на память.

Часть адресного пр-ва под

видеопамять.

Физически видеопамять м.б. расположена в адресной части процессора.

ЦП имеет доступ к видеопамяти через устройство - графический контроллер (интерпретирует поступающие сигналы от ЦП).

Видеопамять м.б. организована следующим образом:

1. страничная видеопамять – цвет на экране в виде суммы основных цветов и каждому отдельному цвету соответствует отдельная страничка видеопамяти.

2. Напрерывная видеопамять – вся информмация о светимости пиксела в виде непрерывного бита, байта и т.д.

С точки зрения процессора видеопамять м.б. большой непрерывной последовательностью байтов или процессор может иметь оконный доступ к видеопамяти, т. е. на адресное пространство процессора отражается окно – в блок видеопамяти нужно установить адрес этого окна перед выводом чего-либо.

Видеоадаптер устроен следующим образом:

VRAM – видеопамять – в основе динамическая память.

GC – графический конроллер – способ доступа прцессора к VRAM может самостоятельно выполняться по командам от процессора, функции по преобразованию VRAM.

SQ - формирует сигналы для отклонения луча для ЭЛТ; управляет выборкой данных у VRAM для отображения.

+ x приращение коор-т.

+y

АС – атрибутный контроллер – управляет преобразованием данных из VRAM в информацию о цвете точки (цвет рамки)

АС поддерживает политру – механизм преобразования кода цвета из VRAM в цвет для ЭЛТ. Политра представляет из себя совокупность регистров политры, данные из VRAM трактуются каак номер регистра.

Регистр содержит информацию о цвете. Регистры могут использоваться для видеоэффектов.

DАС – цифро-аналоговый преобразователь, который из цифрового описания цвета формирует аналоговый сигнал для ЭЛТ.

Будем считать, что VRAM представляет из себя непрерывную область, которая начинаетсяс адреса А.

Изображение формируется из матрицы m X n (m-строк, n-пикселов).На один пиксел – L бит VRAM.

Коор-ты

-адрес VRAM.

L- количество бит на обин пиксель

8 – бит в байте

Изображение формируется в виде матрицы из точек  задача алгоритмов растров. графики – выбрать из множества точек такие, которые бы вызуально максимально соответствовали изображаемому объекту.