Определение видимых точек.

Пусть есть объект, который состоит из D штук примитивов П₁,…,П_d,…,П_D.

K_d - количество поверхностей у примитива с номером d.

К_d – номер какой-то поверхности. К_d=1,…, К_d

S_kd – степень к – той поверхности (=1 или =2)

Если примитив содержит К_d поверхностей, то чтобы определить видимую точку нужно решить К_d систем уравнений:

Каждая из этих систем может вообще не иметь решение  луч и примитив не пересекаются. Иметь одно решение  луч касается примитива либо пересекается в одной точке.

Для квадратичной поверхности 2 решения: луч входит в поверхность и выхобит из неё.

Система имеет бесконечное количество решений. Луч совпадает с поверхностью.

Из найденных решений отбираем те, которые лежат на поверхности примитивов.

Пусть оставшихся точек – В_d (реально всего две)

Нужно отобрать две точки: входная, которая ближе всего к наблюдателю, выходная – дальше всего.

Для каждого примитива нашли две точки: луч входит в пространство п выходит из пространства.

Нужно определить видимые точки для объекта в целом:

Для каждого из примитивов строим матрицу:

 номера поверхностей

Все полученные матрицы объединяем в одну; упорядочив точки по расстоянию от наблюдателя и по таблице, которая выше, определяем принадлежит ли точка комбинации или нет.

Точку нужно дальше закрасить.

Нормаль поверхности grad f (x,y,z), берем источник света и т.д.

Но точка может оказаться затемненной:

Чтобы выявить затененность точки, проводим луч из источника света в точку:

Находим количество решений системы; пусть х_В,, у_В, z_В лежит на поверхности примитива и ближайшая к источнику света, если х_В,, у_В, z_В совпадают, то точка в пределах освещенности, если нет, то в тени.

Изображение основных примитивов методом трассировки лучей.

1. Плоский примитив – часть плоскости, ограниченная ломаной.

уравнение плоскости.

Ломаную линию задаем в виде списка точек:

I. Находим точку пересечения луча и плоскости:

1. луч можно не пересекать с плоскостью

2. совпадать могут  бесконечное число решений

3. в одной точке

1. Решений нет, есл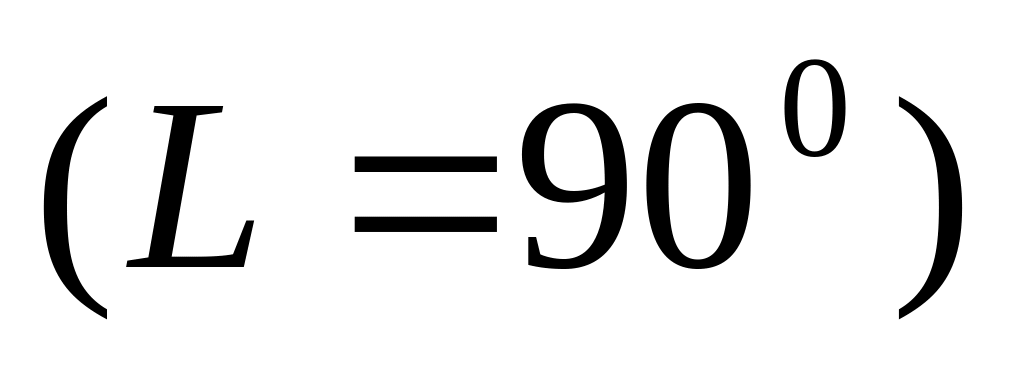и и 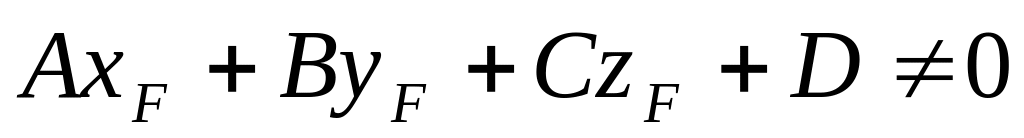(луч параллелен плоскости)

2. и - луч с плдоскостью совпадает  множество решений

3. в одной точке

II. Принадлежит ли найденная точка многоугольнику.

Е сли точка принадлежит многоугольнику, то проекция точки принадлежит проекции многоугольника.

Для выпуклого многоугольника точка лежит внутри, если она по одну сторону от всех ребер. (по часовой стрелке).

Пусть - ребро и

для всех векторов направлена вверх z , то точка внутри.

Векторное произведение 2-х векторов:

Если один и тот же знак, то точка внутри.

Другой способ: соs между векторами.

III. Чтобы окрасить точку, нужно иметь нормаль.

Плоский примитив имеет нулевую толщину  нет внешний и внутренней нормали.

Видимая точка будет освещена,

если наблюдатель и источник примитива

по одну сторону .

По одну сторону, если: